Question

【题目】如图，在△ABC中，D为边BC上一点，AD＝6，BD＝3，DC＝2．

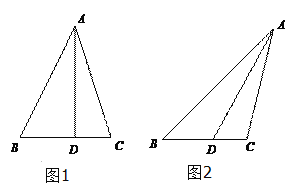
（1）若AD⊥BC，求∠BAC的大小；

（2）若∠ABC＝，求△ADC的面积．

Answer 1

【答案】（1）∠BAC＝．（2） (1＋)

【解析】 试题分析：（1）设，可得，即可求解的值，得到结论；

（2）设，得，在中，由正弦定理，得出，进而得到的值，利用两角和的正弦函数，即可求解结论。

试题解析：

（1）设∠BAD＝α，∠DAC＝β．

因为AD⊥BC，AD＝6，BD＝3，DC＝2，

所以tanα＝，tanβ＝，所以tan∠BAC＝tan(α＋β)＝＝＝1．

又∠BAC∈(0，π)，所以∠BAC＝．

（2）设∠BAD＝α．

在△ABD中，∠ABC＝，AD＝6，BD＝3．

由正弦定理得＝， 解得sinα＝．

因为AD＞BD，所以α为锐角，从而cosα＝＝．

因此sin∠ADC＝sin(α＋)＝sinαcos＋cosαsin

＝ (＋)＝．

△ADC的面积S＝×AD×DC·sin∠ADC

＝×6×2×＝ (1＋)．