题目内容
已知 的图象经过点
的图象经过点 ,且在
,且在 处的切线方程
处的切线方程
(1)求 的解析式;
的解析式;
(2)求 在区间
在区间 上的最大值及取得最大最值时x的值.
上的最大值及取得最大最值时x的值.
(1) ;(2)
;(2) 在区间
在区间 上的最大值为23,当x=-2时取得.
上的最大值为23,当x=-2时取得.
【解析】
试题分析:(1)求导,利用 、
、 ,
, 列出关于
列出关于 的方程组即可求解;(2)求导,列表求最值即可.
的方程组即可求解;(2)求导,列表求最值即可.
解题思路:求函数在闭区间上的最值的一般步骤:第一步,求导;第二步,解 ;第三步,列表(以
;第三步,列表(以 的解划分区间);第四步,比较极值与端点值,得出最值.
的解划分区间);第四步,比较极值与端点值,得出最值.
试题解析:(1)由已知, 1分
1分
把 代入切线方程,得:
代入切线方程,得: ,即切点为(1,-1) 2分
,即切点为(1,-1) 2分
由曲线在 处的切线方程
处的切线方程 ,知:该点处切线的斜率
,知:该点处切线的斜率
求导,得:
令 ① 3分
① 3分
把切点(1,-1)坐标代入原函数,得:
 ② 4分
② 4分
联立①、②解出: 5分
5分
∴ 6分
6分
(2)由(1)知:
求导,得: 7分
7分
令: 8分
8分
【解析】 或
或 即得:
即得: 9分
9分
列表:列出x∈ 函数区间 11分
函数区间 11分
x | 2 |
|
|
| 0 |
|
|
| 1 |
y’ | - | + | - | + | |||||
y | 23 |
|
|
| 1 |
|
|
| -1 |
由表可知: 在区间
在区间 上的最大值为23,当x=-2时取得。 12分
上的最大值为23,当x=-2时取得。 12分
考点:1.导数的几何意义;2.函数在闭区间上的最值.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目









 有公共焦点,且离心率
有公共焦点,且离心率 的双曲线方程为( )
的双曲线方程为( ) B.
B.
 D.
D.
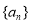 是等比数列,其前n项和为
是等比数列,其前n项和为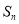 ,若
,若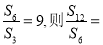 ( )
( ) +
+ ,
, ∈(0,π),则tan
∈(0,π),则tan 的最小正周期为 .
的最小正周期为 . 在点M处的瞬时变化率为-4,则点M的坐标是___________.
在点M处的瞬时变化率为-4,则点M的坐标是___________. B.
B. C.
C. D.
D.
 、
、 满足条件
满足条件 ,则
,则 的最小值为___________;
的最小值为___________;  、
、 两点之间的距离为7,则
两点之间的距离为7,则 =_______.
=_______.