题目内容
在平面直角坐标系xOy中,已知点A(-1,0),B(1,0),动点C满足条件:△ABC的周长为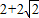 ,记动点C的轨迹为曲线W.
,记动点C的轨迹为曲线W.(1)求W的方程;
(2)曲线W上是否存在这样的点P:它到直线x=-1的距离恰好等于它到点B的距离?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】分析:(1)根据△ABC的周长为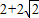 ,|AB|=2,利用椭圆的定义可得动点C的轨迹,从而可得W的方程;
,|AB|=2,利用椭圆的定义可得动点C的轨迹,从而可得W的方程;
(2)假设存在点P满足题意,则点P为抛物线y2=4x与曲线W: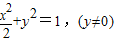 的交点,联立方程,求得交点即可.
的交点,联立方程,求得交点即可.
解答:解:(1)设C(x,y),∵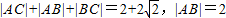 ,
,
∴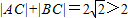 …(3分)
…(3分)
∴由椭圆的定义知,动点C的轨迹是以A、B为焦点,长轴长为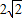 的椭圆(除去与x轴的两个交点).
的椭圆(除去与x轴的两个交点).
∴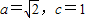 ,∴b2=a2-c2=1…(5分)
,∴b2=a2-c2=1…(5分)
∴W的方程: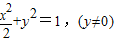 …(6分)
…(6分)
(2)假设存在点P满足题意,则点P为抛物线y2=4x与曲线W: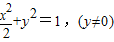 的交点,
的交点,
由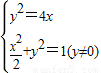 ,消去y得:x2+8x-2=0…(9分)
,消去y得:x2+8x-2=0…(9分)
解得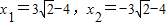 (舍去) …(11分)
(舍去) …(11分)
由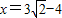 代入抛物线的方程得
代入抛物线的方程得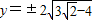 …(13分)
…(13分)
所以存在两个点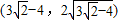 和
和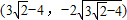 满足题意.…(14分)
满足题意.…(14分)
点评:本题考查椭圆的定义,考查椭圆的标准方程,考查曲线的交点,考查学生的计算能力,属于中档题.
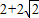 ,|AB|=2,利用椭圆的定义可得动点C的轨迹,从而可得W的方程;
,|AB|=2,利用椭圆的定义可得动点C的轨迹,从而可得W的方程;(2)假设存在点P满足题意,则点P为抛物线y2=4x与曲线W:
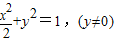 的交点,联立方程,求得交点即可.
的交点,联立方程,求得交点即可.解答:解:(1)设C(x,y),∵
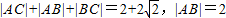 ,
,∴
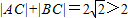 …(3分)
…(3分)∴由椭圆的定义知,动点C的轨迹是以A、B为焦点,长轴长为
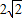 的椭圆(除去与x轴的两个交点).
的椭圆(除去与x轴的两个交点).∴
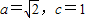 ,∴b2=a2-c2=1…(5分)
,∴b2=a2-c2=1…(5分)∴W的方程:
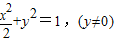 …(6分)
…(6分)(2)假设存在点P满足题意,则点P为抛物线y2=4x与曲线W:
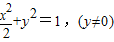 的交点,
的交点,由
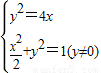 ,消去y得:x2+8x-2=0…(9分)
,消去y得:x2+8x-2=0…(9分)解得
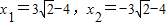 (舍去) …(11分)
(舍去) …(11分)由
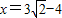 代入抛物线的方程得
代入抛物线的方程得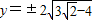 …(13分)
…(13分)所以存在两个点
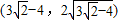 和
和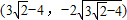 满足题意.…(14分)
满足题意.…(14分)点评:本题考查椭圆的定义,考查椭圆的标准方程,考查曲线的交点,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是