题目内容
19.已知数列{an}中,若a1=0,ai=k2(i∈N*,2k≤i<2k+1,k=1,2,3,…),则满足ai+a2i≥100的i的最小值为128.
分析 由题意可得ai+a2i=k2+(k+1)2≥100,从而解得.
解答 解:∵ai=k2(i∈N*,2k≤i<2k+1,k=1,2,3,…),
∴ai+a2i=k2+(k+1)2≥100,
故k≥7;
故i的最小值为27=128,
故答案为:128.
点评 本题考查了数列,注意i与2i的关系对k的影响即可.

练习册系列答案
相关题目
9.已知定义在R上的函数f(x)满足:y=f(x-1)的图象关于(1,0)点对称,且当x≥0时恒有f(x+2)=f(x),当x∈[0,2)时,f(x)=ex-1,则f(2016)+f(-2015)=( )
| A. | 1-e | B. | e-1 | C. | -1-e | D. | e+1 |
10. 执行如图所示的程序框图,若输入的M的值为55,则输出的i的值为( )
执行如图所示的程序框图,若输入的M的值为55,则输出的i的值为( )
 执行如图所示的程序框图,若输入的M的值为55,则输出的i的值为( )
执行如图所示的程序框图,若输入的M的值为55,则输出的i的值为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
4.执行如图所示的程序框图,输出c的结果为( )
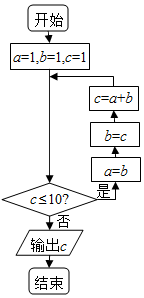

| A. | 13 | B. | 21 | C. | 17 | D. | 15 |
8.已知函数f(x)=sin(2x+φ)(|φ|<π)的图象过点P(0,$\frac{1}{2}$),如图,则φ的值为( )
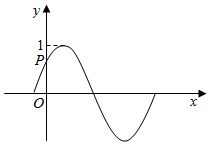

| A. | $\frac{π}{6}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{6}$或$\frac{5π}{6}$ | D. | -$\frac{π}{6}$或$\frac{5π}{6}$ |
