题目内容
已知函数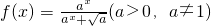
(1)求f(x)+f(1-x)及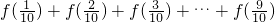 的值;
的值;
(2)是否存在自然数a,使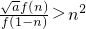 对一切n∈N都成立,若存在,求出自然数a的最小值;不存在,说明理由;
对一切n∈N都成立,若存在,求出自然数a的最小值;不存在,说明理由;
(3)利用(2)的结论来比较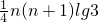 和lg(n!)(n∈N)的大小.
和lg(n!)(n∈N)的大小.
解:(1)f(x)+f(1-x)
=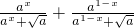
=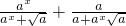
=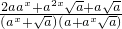
=1.
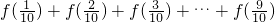
=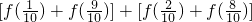 +
+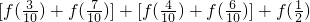
=4+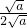
= .
.
(2)假设存在自然数a,使 对一切n∈N都成立.
对一切n∈N都成立.
由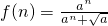 ,
,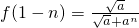
得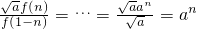 ,
,
当a=1,2时,不等式an>n2显然不成立.
当a≥3时,an≥3n>n2,
当n=1时,显然3>1,
当n≥2时,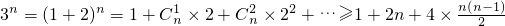 =2n2+1>n2成立,
=2n2+1>n2成立,
则 3n>n2对一切n∈N都成立.
所以存在最小自然数a=3.
(3)由3n>n2?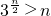 (n∈N),
(n∈N),
所以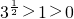 ,
,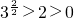 ,…,
,…,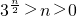 ,
,
相乘得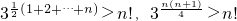 ,
,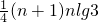 >lgn!成立.
>lgn!成立.
分析:(1)f(x)+f(1-x)=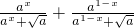 =
=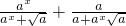 =1.
=1.
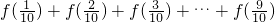 =
=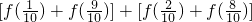 +
+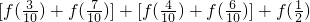 =4+
=4+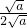 ,由此能求出其结果.
,由此能求出其结果.
(2)假设存在自然数a,使 对一切n∈N都成立.由
对一切n∈N都成立.由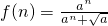 ,
,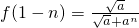 得
得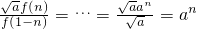 ,由此能够证明存在最小自然数a=3.
,由此能够证明存在最小自然数a=3.
(3)由3n>n2?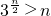 (n∈N),所以
(n∈N),所以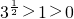 ,
,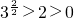 ,…,
,…,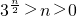 ,由此能比较
,由此能比较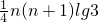 和lg(n!)(n∈N)的大小.
和lg(n!)(n∈N)的大小.
点评:本题考查不等式的综合应用,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.
=
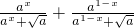
=
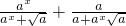
=
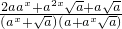
=1.
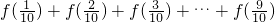
=
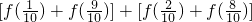 +
+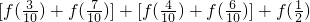
=4+
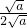
=
 .
.(2)假设存在自然数a,使
 对一切n∈N都成立.
对一切n∈N都成立.由
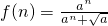 ,
,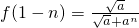
得
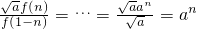 ,
,当a=1,2时,不等式an>n2显然不成立.
当a≥3时,an≥3n>n2,
当n=1时,显然3>1,
当n≥2时,
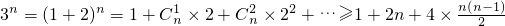 =2n2+1>n2成立,
=2n2+1>n2成立,则 3n>n2对一切n∈N都成立.
所以存在最小自然数a=3.
(3)由3n>n2?
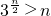 (n∈N),
(n∈N),所以
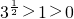 ,
,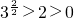 ,…,
,…,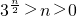 ,
,相乘得
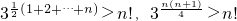 ,
,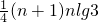 >lgn!成立.
>lgn!成立.分析:(1)f(x)+f(1-x)=
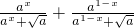 =
=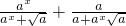 =1.
=1.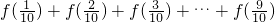 =
=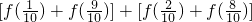 +
+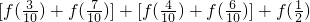 =4+
=4+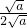 ,由此能求出其结果.
,由此能求出其结果.(2)假设存在自然数a,使
 对一切n∈N都成立.由
对一切n∈N都成立.由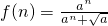 ,
,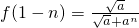 得
得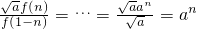 ,由此能够证明存在最小自然数a=3.
,由此能够证明存在最小自然数a=3.(3)由3n>n2?
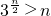 (n∈N),所以
(n∈N),所以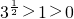 ,
,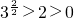 ,…,
,…,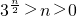 ,由此能比较
,由此能比较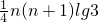 和lg(n!)(n∈N)的大小.
和lg(n!)(n∈N)的大小.点评:本题考查不等式的综合应用,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目


 上恒成立,求实数m的取值范围.
上恒成立,求实数m的取值范围.

