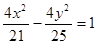题目内容
如果直线 与圆
与圆 交于M,N两点,且M,N关于直线
交于M,N两点,且M,N关于直线 对称,动点P(a,b)在不等式组
对称,动点P(a,b)在不等式组 表示的平面区域内部及边界上运动,则
表示的平面区域内部及边界上运动,则 取值范围是( )
取值范围是( )
A. | B. | C. | D.   |
D
解析试题分析:∵M,N是圆上两点,且M,N关于直线2x-y=0对称,
∴直线2x-y=0经过圆的圆心( ,
, ),且直线2x-y=0与直线y=kx+1垂直.
),且直线2x-y=0与直线y=kx+1垂直.
∴k= ,m=-1.
,m=-1.
∴约束条件为
根据约束条件画出可行域,
 表示可行域内点Q和点P(1,2)连线的斜率,
表示可行域内点Q和点P(1,2)连线的斜率,
当Q点在原点O时,直线PQ的斜率为2,当Q点在可行域内的点B(4,0)处时,直线PQ的斜率为 ,
,
结合直线PQ的位置可得,当点Q在可行域内运动时,其斜率的取值范围是: ∪[2,+∞)
∪[2,+∞)
从而得到w的取值范围 ∪[2,+∞).
∪[2,+∞).
故选D.
考点:本题主要考查轴对称问题,简单的线性规划,以及利用几何意义求最值。
点评:中档题.巧妙识别目标函数的几何意义是我们研究规划问题的基础,能依题意首先求得m,k是解题的关键,使得规划问题得以深化.

练习册系列答案
相关题目
已知 为圆
为圆 内异于圆心的一点,则直线
内异于圆心的一点,则直线 与该圆的位置关系是 ( )
与该圆的位置关系是 ( )
| A.相切 | B.相交 | C.相离 | D.相切或相交 |
若直线 始终平分圆
始终平分圆 的周长,则
的周长,则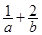 的最小值为
的最小值为
| A.1 | B.5 | C.3+ | D. |
已知圆 及直线
及直线 当直线
当直线 被圆
被圆 截得的弦长为
截得的弦长为 ,则
,则 ( )
( )
A. | B. | C. | D. |
当点P在圆x2+y2=1上变动时,它与定点Q (3,0) 相连,线段PQ的中点M的轨迹方程是( )
| A.(x+3)2+y2=4 | B.(x-3)2+y2=1 |
| C.(2x-3)2+4y2=1 | D.(2x+3)2+4y2=1 |
设 ,若线段
,若线段 是△
是△ 外接圆的直径,则点
外接圆的直径,则点 的坐标是( ).
的坐标是( ).
| A.(-8,6) | B.(8,-6) | C.(4,-6) | D.(4,-3) |
若直线 (
( )被圆
)被圆 截得的弦长为4,则
截得的弦长为4,则 的最小值为( )
的最小值为( )
A. | B. | C.2 | D.4 |
已知直线 与圆
与圆 交于
交于 两点,且
两点,且 ,则实数
,则实数 的值为( )
的值为( )
| A.2 | B.-2 | C.2或-2 | D. 或 或 |
 的圆心为C,A(1,0)是圆内一定点,Q为圆周上任一点.线段AQ的垂直平分线与CQ的连线交于点M,则M的轨迹方程为( ).
的圆心为C,A(1,0)是圆内一定点,Q为圆周上任一点.线段AQ的垂直平分线与CQ的连线交于点M,则M的轨迹方程为( ).