题目内容
若a、b是正数,则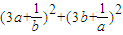 的最小值为 .
的最小值为 .
【答案】分析:连续用基本不等式求最小值,由题设知 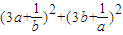 ≥2(
≥2(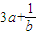 )(
)(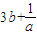 )=2(9ab+
)=2(9ab+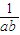 )+12,其中等号成立的条件是a=b,又(9ab+
)+12,其中等号成立的条件是a=b,又(9ab+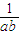 )≥
)≥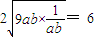 .
.
等号成立的条件是条件是9ab=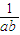 与a=b联立得两次运用基本不等式等号成立的条件是x=y=
与a=b联立得两次运用基本不等式等号成立的条件是x=y=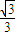 ,计算出最值是24.
,计算出最值是24.
解答:解:∵a,b是正数,
∴ ≥2(
≥2(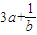 )(
)(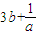 )=2(9ab+
)=2(9ab+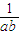 )+12
)+12
等号成立的条件是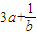 =
=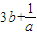
解得a=b,①
又(9ab+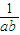 )≥
)≥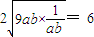 .
.
等号成立的条件是9ab=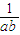 ②
②
由①②联立解得x=y=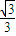 ,
,
即当x=y=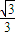 时,
时,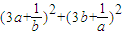 的最小值为2×+12=24
的最小值为2×+12=24
故答案为:24
点评:本题考查基本不等式,解题过程中两次运用基本不等式,注意验证两次运用基本不等式时等号成立的条件是否相同,若相同时,代数式才能取到计算出的最小值,否则最小值取不到.本题是一道易错题.
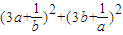 ≥2(
≥2(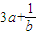 )(
)(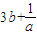 )=2(9ab+
)=2(9ab+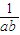 )+12,其中等号成立的条件是a=b,又(9ab+
)+12,其中等号成立的条件是a=b,又(9ab+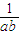 )≥
)≥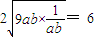 .
.等号成立的条件是条件是9ab=
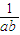 与a=b联立得两次运用基本不等式等号成立的条件是x=y=
与a=b联立得两次运用基本不等式等号成立的条件是x=y=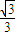 ,计算出最值是24.
,计算出最值是24.解答:解:∵a,b是正数,
∴
 ≥2(
≥2(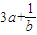 )(
)(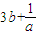 )=2(9ab+
)=2(9ab+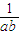 )+12
)+12等号成立的条件是
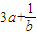 =
=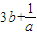
解得a=b,①
又(9ab+
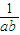 )≥
)≥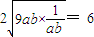 .
.等号成立的条件是9ab=
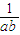 ②
②由①②联立解得x=y=
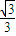 ,
,即当x=y=
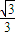 时,
时,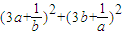 的最小值为2×+12=24
的最小值为2×+12=24故答案为:24
点评:本题考查基本不等式,解题过程中两次运用基本不等式,注意验证两次运用基本不等式时等号成立的条件是否相同,若相同时,代数式才能取到计算出的最小值,否则最小值取不到.本题是一道易错题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
若a、b是正数,则
、
、
、
这四个数的大小顺序是( )
| a+b |
| 2 |
| ab |
| 2ab |
| a+b |
|
A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|
 的最小值为________.
的最小值为________. 的最小值为 .
的最小值为 .