题目内容
如图,直角梯形ABCD中, A=90°,
A=90°, B=45°,底边AB=5,高AD=3,点E由B沿折线BCD向点D移动,EM
B=45°,底边AB=5,高AD=3,点E由B沿折线BCD向点D移动,EM AB于M,EN
AB于M,EN AD于N,设BM=
AD于N,设BM=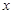 ,矩形AMEN的面积为
,矩形AMEN的面积为 ,那么
,那么 与
与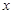 的函数关系的图像大致是( )
的函数关系的图像大致是( )

A
解析试题分析:根据已知可得:点E在未到达C之前,y=x(5-x)=5x-x2;且x≤3,当x从0变化到2.5时,y逐渐变大,
当x=2.5时,y有最大值,当x从2.5变化到3时,y逐渐变小,
到达C之后,y=3(5-x)=15-3x,x>3,
根据二次函数和一次函数的性质.故选:A.
考点:动点问题的函数图象;二次函数的图象.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
已知函数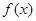 在[0,+∞]上是增函数,
在[0,+∞]上是增函数,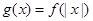 ,若
,若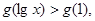 则
则 的取值范围是( )
的取值范围是( )
A.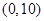 | B.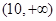 |
C.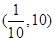 | D.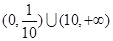 |
函数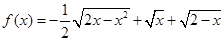 的最大值为( )
的最大值为( )
A.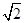 | B.2 | C.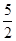 | D.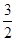 |
已知函数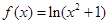 的值域为
的值域为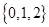 ,则满足这样条件的函数的个数有( )个.
,则满足这样条件的函数的个数有( )个.
| A.8 | B.9 | C.26 | D.27 |
已知函数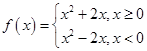 ,若
,若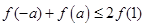 ,则实数
,则实数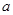 的取值范围是( )
的取值范围是( )
A.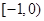 | B.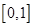 | C.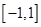 | D. |
函数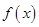 的部分图象如图所示,则
的部分图象如图所示,则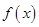 的解析式可以是
的解析式可以是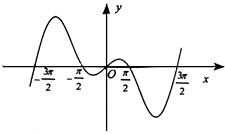
A.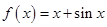 | B.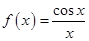 |
C.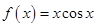 | D. |
若函数f(x)=a|2x-4|(a>0,a≠1)满足f(1)=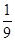 ,则f(x)的单调递减区间是( )
,则f(x)的单调递减区间是( )
| A.(-∞,2] | B.[2,+∞) |
| C.[-2,+∞) | D.(-∞,-2] |
若f(x)=- x2+bln(x+2)在(-1,+∞)上是减函数,则b的取值范围是( )
x2+bln(x+2)在(-1,+∞)上是减函数,则b的取值范围是( )
| A.[-1,+∞) | B.(-1,+∞) |
| C.(-∞,-1] | D.(-∞,-1) |