题目内容

已知函数f(x)=x+
ax

（1）若f（2）=4，求a的值；
（2）x＞0时，f（x）的图象如图，看图指出y=f（x）（x＞0）的减区间，并证明你的结论．
（3）请根据函数的性质画出f（x）（x＜0）的草图（无需列表）．
分析：（1）把x=2代入f（x），求得a的值；
（2）由图象得y=f（x）（x＞0）的减区间，用定义证明f（x）的单调性；
（3）f（x）是定义域上的奇函数，图象关于原点对称，根据x＞0时f（x）的图象，可以画出x＜0时f（x）的图象．
解答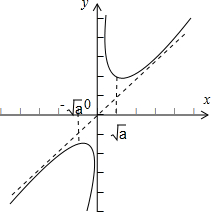：解：（1）∵f(2)=2+
a
2
=4∴a=4，即a的值是4；
（2）由图知，y=f（x）（x＞0）的减区间是(0，
a
)
证明：设任意的x1，x2，且0＜x1＜x2＜
a
；
则f（x1）-f（x2）=（x1+
a
x1
）-（x2+
a
x2
）=(x1-x2)(1-
a
x1x2
)=(x1-x2)(
x1x2-a
x1x2
)；
∵0＜x1＜x2＜
a
，∴x1x2＜a，∴x1x2-a＜0，
∴f（x1）-f（x2）＜0；
∴f（x）在(0，
a
)上单调递减．
（3）∵函数f(x)=x+
a
x
（x≠0），∴f（-x）=-x+
a
-x
=-（x+
a
x
）=-f（x），
∴f（x）是定义域上的奇函数，图象关于原点对称；
根据x＞0时f（x）的图象，画出x＜0时f（x）的图象，如图．
点评：本题考查了基本初等函数的性质与应用问题，根据函数的图象写出单调性以及应用奇偶性画出函数的图象等知识，是基础题．
练习册系列答案
相关题目
已知函数f(x)=x-2m2+m+3(m∈Z)为偶函数，且f（3）＜f（5）．
（1）求m的值，并确定f（x）的解析式；
（2）若g（x）=loga[f（x）-ax]（a＞0且a≠1），是否存在实数a，使g（x）在区间[2，3]上的最大值为2，若存在，请求出a的值，若不存在，请说明理由．
（2011•上海模拟）已知函数f(x)=(
x
a
-1)2+(
b
x
-1)2，x∈(0，+∞)，其中0＜a＜b．
（1）当a=1，b=2时，求f（x）的最小值；
（2）若f（a）≥2m-1对任意0＜a＜b恒成立，求实数m的取值范围；
（3）设k、c＞0，当a=k2，b=（k+c）2时，记f（x）=f1（x）；当a=（k+c）2，b=（k+2c）2时，记f（x）=f2（x）．
求证：f1(x)+f2(x)＞
4c2
k(k+c)
．

已知函数f(x)的图像在[a，b]上连续不断，f1(x)＝min{f(t)|a≤t≤x}(x∈[a，b])，f2(x)＝max{f(t)|a≤t≤x}(x∈[a，b])，其中，min{f(x)|x∈D}表示函数f(x)在D上的最小值，max{f(x)|x∈D}表示函数f(x)在D上的最大值，若存在最小正整数k，使得f2(x)－f1(x)≤k(x－a)对任意的x∈[a，b]成立，则称函数f(x)为[a，b]上的“k阶收缩函数”．已知函数f(x)＝x2，x∈[－1，4]为[－1，4]上的“k阶收缩函数”，则k的值是_________．
已知函数f(x)=(
x
a
-1)2+(
b
x
-1)2，x∈(0，+∞)，其中0＜a＜b．
（1）当a=1，b=2时，求f（x）的最小值；
（2）若f（a）≥2m-1对任意0＜a＜b恒成立，求实数m的取值范围；
（3）设k、c＞0，当a=k2，b=（k+c）2时，记f（x）=f1（x）；当a=（k+c）2，b=（k+2c）2时，记f（x）=f2（x）．
求证：f1(x)+f2(x)＞
4c2
k(k+c)
．
已知函数f（x）、g（x），下列说法正确的是（ ）
A．f（x）是奇函数，g（x）是奇函数，则f（x）+g（x）是奇函数
B．f（x）是偶函数，g（x）是偶函数，则f（x）+g（x）是偶函数
C．f（x）是奇函数，g（x）是偶函数，则f（x）+g（x）一定是奇函数或偶函数
D．f（x）是奇函数，g（x）是偶函数，则f（x）+g（x）可以是奇函数或偶函数

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网