题目内容
如图，直三棱柱ABC－A1B1C1的底面ABC为等腰直角三角形，∠ACB＝90°，AC＝1，C点到AB1的距离为CE＝
，D为AB的中点．
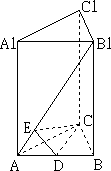
(1)求证：AB1⊥平面CED；
(2)求异面直线AB1与CD之间的距离
答案：
解析：
解析：
(1)∵D是AB中点，△ABC为等腰直角三角形，∠ABC＝900，∴CD⊥AB又AA1⊥平面ABC，∴CD⊥AA1．
∴CD⊥平面A1B1BA ∴CD⊥AB1，又CE⊥AB1，∴AB1⊥平面CDE；
(2)由CD⊥平面A1B1BA ∴CD⊥DE
∵AB1⊥平面CDE ∴DE⊥AB1
∴DE是异面直线AB1与CD的公垂线段
∵CE＝
，AC＝1，∴CD＝
∴
；
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，直三棱柱ABC-A1B1C1中，
如图，直三棱柱ABC-A1B1C1中，底面是以∠ABC为直角的等腰直角三角形，AC=2a，BB1=3a，D为A1C1的中点，E为B1C的中点．
如图在直三棱柱ABC-A1B1C1中∠ACB=90°，AA1=2，AC=BC=1，则异面直线A1B与AC所成角的余弦值是
如图，直三棱柱ABC-A1B1C1中，AC⊥BC，AC=BC=CC1=2，M，N分别为AC，B1C1的中点．
如图，直三棱柱ABC-A1B1C1中，∠BAC=90°，AB=AC=a，AA1=2a，D棱B1B的中点．