题目内容
已知函数 为偶函数,其图象与x轴的交点为x1,x2,若|x1-x2|的最小值为
为偶函数,其图象与x轴的交点为x1,x2,若|x1-x2|的最小值为 ,则该函数的一个递增区间可以是( )
,则该函数的一个递增区间可以是( )A.

B.

C.

D.

【答案】分析:由函数是偶函数及θ的范围求出θ的值,再由|x2-x1|的最小值为π,得到w的值,从而得到函数的解析式,由函数的解析式求得该函数的递增区间.
解答:解:∵y= sin(wx+α)为偶函数,∴α=
sin(wx+α)为偶函数,∴α= +kπ k∈z,又∵0<α<π,∴α=
+kπ k∈z,又∵0<α<π,∴α= .
.
由诱导公式得函数y=2coswx. 又∵其图象与直线y=2某两个交点的横坐标分别为x1,x2,∵|x2-x1|的最小值为π,
∴函数的周期为π,即 w=2,∴y=2cos2x,∴函数在 上为增函数.
上为增函数.
故选:C.
点评:本题考查的是三角函数及函数的奇偶性的综合知识,解答关键是应用数学中的数形结合的思想方法.
解答:解:∵y=
 sin(wx+α)为偶函数,∴α=
sin(wx+α)为偶函数,∴α= +kπ k∈z,又∵0<α<π,∴α=
+kπ k∈z,又∵0<α<π,∴α= .
.由诱导公式得函数y=2coswx. 又∵其图象与直线y=2某两个交点的横坐标分别为x1,x2,∵|x2-x1|的最小值为π,
∴函数的周期为π,即 w=2,∴y=2cos2x,∴函数在
 上为增函数.
上为增函数.故选:C.
点评:本题考查的是三角函数及函数的奇偶性的综合知识,解答关键是应用数学中的数形结合的思想方法.

练习册系列答案
相关题目
已知函数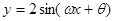 为偶函数
为偶函数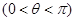 ,其图像与直线
,其图像与直线 的某两个交点的横坐标为
的某两个交点的横坐标为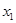 ,
,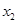 ,若
,若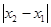 的最小值为
的最小值为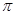 ,则( )
,则( )
A.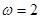 , ,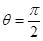 | B.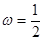 , ,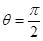 |
C.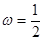 , ,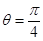 | D.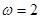 , ,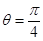 |
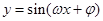
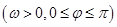 为偶函数,其图象上相邻两个最高点之间的距离为
为偶函数,其图象上相邻两个最高点之间的距离为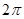 .
.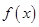 的解析式.
的解析式.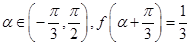 ,求
,求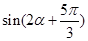 的值.
的值.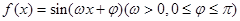 为偶函数,其图象上相邻的两个最高点之间的距离为
为偶函数,其图象上相邻的两个最高点之间的距离为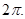
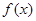 的解析式;
的解析式; 的值。
的值。 为偶函数
为偶函数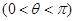 ,其图像与直线
,其图像与直线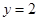 的某两个交点的横坐标为
的某两个交点的横坐标为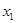 ,
,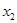 ,若
,若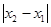 的最小值为
的最小值为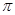 ,则( )
,则( )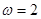 ,
,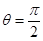 B.
B.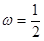 ,
,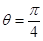 D.
D.