题目内容
19.如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=3,AD=2,AB=2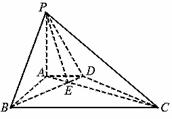
(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)求二面角P-BD-A的大小.
解法一:(1)∵PA⊥平面ABCD,BD![]() 平面ABCD,∴BD⊥PA.
平面ABCD,∴BD⊥PA.
又tan∠ABD=![]() ,tan∠BAC=
,tan∠BAC=![]() =
=![]() ,
,
∴∠ABD=30°,∠BAC=60°.
∴∠AEB=90°,即BD⊥AC.
又PA∩AC=A,
∴BD⊥平面PAC.

(2)连结PE,
∵BD⊥平面PAC,∴BD⊥PE,BD⊥AE.
∴∠AEP为二面角P-BD-A的平面角.
在Rt△AEB中,AE=AB·sin∠ABD=![]() ,
,
∴tan∠AEP=![]() =
=![]() .∴∠AEP=60°.
.∴∠AEP=60°.
∴二面角P-BD-A的大小为60°.
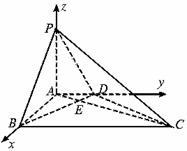
解法二:(1)如图,建立坐标系,则A(0,0,0),B(2![]() ,0,0),C(2
,0,0),C(2![]() ,6,0),D(0,2,0),P(0,0,3),
,6,0),D(0,2,0),P(0,0,3),
∴![]() =(0,0,3),
=(0,0,3), ![]() =(2
=(2![]() ,6,0),
,6,0),![]() =(-2
=(-2![]() ,2,0).
,2,0).
∴![]() ·
·![]() =0,
=0, ![]() ·
·![]() =0.
=0.
∴BD⊥AP,BD⊥AC.
又PA∩AC=A,∴BD⊥平面PAC.
(2)取平面ABD的法向量为m=(0,0,1),
设平面PBD的法向量为n=(x,y,1),
则n·![]() =0,n·
=0,n·![]() =0,
=0,
∴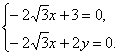 解得
解得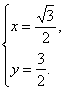
∴n=(![]() ,
,![]() ,1).
,1).
∴cos〈m,n〉=![]() =
=![]() .
.
∴二面角P-BD-A的大小为60°.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 如图,已知棱锥P-ABCD的底面ABCD为直角梯 形,AB∥CD,AB⊥BC,CD=PB=BC=1,
如图,已知棱锥P-ABCD的底面ABCD为直角梯 形,AB∥CD,AB⊥BC,CD=PB=BC=1, 如图,在四棱锥P-ABCD中,底面为直角梯ABCD,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M,N分别为PC,PB的中点.
如图,在四棱锥P-ABCD中,底面为直角梯ABCD,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M,N分别为PC,PB的中点. 如图,在四棱锥P-ABCD中,底面为直角梯ABCD,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M,N分别为PC,PB的中点.
如图,在四棱锥P-ABCD中,底面为直角梯ABCD,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M,N分别为PC,PB的中点.
