题目内容
15.在圆x2+y2-4x-4y-2=0内,过点E(0,1)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为( )| A. | 5$\sqrt{2}$ | B. | 10$\sqrt{2}$ | C. | 15$\sqrt{2}$ | D. | 20$\sqrt{2}$ |
分析 把圆的方程化为标准方程后,找出圆心坐标与圆的半径,根据图形可知,过点E最长的弦为直径AC,最短的弦为过E与直径AC垂直的弦BD,根据两点间的距离公式求出ME的长度,根据垂径定理得到E为BD的中点,在直角三角形BME中,根据勾股定理求出BE,则BD=2BE,然后利用AC与BD的乘积的一半即可求出四边形ABCD的面积.
解答 解:把圆的方程化为标准方程得:(x-2)2+(y-2)2=10,
则圆心坐标为(2,2),半径为$\sqrt{10}$,
根据题意画出图象,如图所示:
由图象可知:过点E最长的弦为直径AC,最短的弦为过E与直径AC垂直的弦,则AC=2$\sqrt{10}$,MB=$\sqrt{10}$,ME=$\sqrt{(2-0)^{2}+(2-1)^{2}}$=$\sqrt{5}$,
所以BD=2BE=2$\sqrt{5}$,
又AC⊥BD,
所以四边形ABCD的面积S=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×2$\sqrt{10}$×2$\sqrt{5}$=10$\sqrt{2}$.
故选B
点评 此题考查学生掌握垂径定理及勾股定理的应用,灵活运用两点间的距离公式化简求值,是一道中档题.学生做题时注意对角线垂直的四边形的面积等于对角线乘积的一半.

练习册系列答案
相关题目
3.下列说法正确的是( )
| A. | 某人打靶,射击10次,击中7次,那么此人中靶的概率为0.7 | |
| B. | 一位同学做掷硬币试验,掷6次,一定有3次“正面朝上” | |
| C. | 某地发行福利彩票,回报率为47%,有人花了100元钱买彩票,一定会有47元的回报 | |
| D. | 概率等于1的事件不一定为必然事件 |
10.若集合M={1,2,3},N={x|0<x≤3,x∈R},则下列论断正确的是( )
| A. | x∈M是x∈N的充分不必要条件 | B. | x∈M是x∈N的必要不充分条件 | ||
| C. | x∈M是x∈N 的充分必要条件 | D. | x∈M是x∈N的既不充分也不必要条件 |
7.设x∈R,记不超过x的最大整数为[x],如[2.5]=2,[-2.5]=-3,令{x}=x-[x],则{$\frac{\sqrt{5}+1}{2}$},[$\frac{\sqrt{5}+1}{2}$],$\frac{\sqrt{5}+1}{2}$,三个数构成的数列( )
| A. | 是等比数列但不是等差数列 | B. | 是等差数列但不是等比数列 | ||
| C. | 既是等差数列又是等比数列 | D. | 既不是等差数列也不是等比数列 |
5.若函数f(x)唯一的一个零点同时在区间(0,8)、(0,6)、(0,4)、(0,2)内,那么下列命题中正确的是( )
| A. | 函数f(x)在区间(0,1)内有零点 | B. | 函数f(x)在区间(0,1)或(1,2)内有零点 | ||
| C. | 函数f(x)在区间[2,8)内无零点 | D. | 函数f(x)在区间(1,8)内无零点 |
 四边形OABC的四个顶点坐标分别为O(0,0),A(6,2),B(4,6),C(2,6),直线y=kx($\frac{1}{3}$<k<3)把四边形OABC分成两部分,S表示靠近x轴一侧那部分的面积.
四边形OABC的四个顶点坐标分别为O(0,0),A(6,2),B(4,6),C(2,6),直线y=kx($\frac{1}{3}$<k<3)把四边形OABC分成两部分,S表示靠近x轴一侧那部分的面积.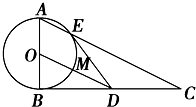 如图,△ABC是直角三角形,∠ABC=90°,以AB为直径的圆O交AC于点E,过E作圆的切线交BC于D点.连结OD交圆O于点M.
如图,△ABC是直角三角形,∠ABC=90°,以AB为直径的圆O交AC于点E,过E作圆的切线交BC于D点.连结OD交圆O于点M.