题目内容
已知函数 .
.
(1)当0<a<b,且f(a)=f(b)时,求证:ab>1;
(2)是否存在实数a、b,(a<b),使得函数y=f(x)的定义域是[a,b],值域是 ,若存在,则求出a、b的值;若不存在,请说明理由.
,若存在,则求出a、b的值;若不存在,请说明理由.
解:(1)证明:∵0<a<b,且f(a)=f(b),∴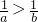 >0.
>0.
∴1- =-(1-
=-(1- ),∴2=
),∴2= +
+ >2
>2 ,∴
,∴ <1,∴ab>1.
<1,∴ab>1.
(2)由函数y=f(x)的定义域是[a,b],值域是 ,
,
当1≤a<b 时,可得 =1-
=1- 在[a,b]上是增函数,故有 1-
在[a,b]上是增函数,故有 1- =
= a,1-
a,1- =
= b,
b,
解得 a= ,b=
,b= .
.
当0<a<b≤1时,可得 =
= -1 在[a,b]上是减函数,故有
-1 在[a,b]上是减函数,故有 =
= ,
, =
= ,
,
解得 a= ,b=
,b= (不合题意舍去).
(不合题意舍去).
当0<a<1<b时,函数y=f(x)在定义域[a,b]上的最小值为0,根据值域是 ,
,
可得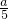 =0,a=0 (不合题意舍去).
=0,a=0 (不合题意舍去).
综上,存在a= ,b=
,b= 满足条件.
满足条件.
分析:(1)根据条件可得1- =-(1-
=-(1- ),即2=
),即2= +
+ ,利用基本不等式可得
,利用基本不等式可得 <1,从而得到ab>1.
<1,从而得到ab>1.
(2)当1≤a<b 时,可得 =1-
=1- 在[a,b]上是增函数,故有 1-
在[a,b]上是增函数,故有 1- =
= a,1-
a,1- =
= b,解出a、b的值.
b,解出a、b的值.
当0<a<b≤1时,可得 =
= -1 在[a,b]上是减函数,故有
-1 在[a,b]上是减函数,故有 =
= ,
, =
= ,解得a、b 无解.
,解得a、b 无解.
当0<a<1<b时,函数y=f(x)在定义域[a,b]上的最小值为0,根据值域是 ,解得a、b 无解.
,解得a、b 无解.
点评:本题主要考查求函数的定义域、值域,带绝对值的函数,体现了分类讨论的数学思想.
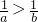 >0.
>0.∴1-
 =-(1-
=-(1- ),∴2=
),∴2= +
+ >2
>2 ,∴
,∴ <1,∴ab>1.
<1,∴ab>1.(2)由函数y=f(x)的定义域是[a,b],值域是
 ,
,当1≤a<b 时,可得
 =1-
=1- 在[a,b]上是增函数,故有 1-
在[a,b]上是增函数,故有 1- =
= a,1-
a,1- =
= b,
b,解得 a=
 ,b=
,b= .
.当0<a<b≤1时,可得
 =
= -1 在[a,b]上是减函数,故有
-1 在[a,b]上是减函数,故有 =
= ,
, =
= ,
,解得 a=
 ,b=
,b= (不合题意舍去).
(不合题意舍去).当0<a<1<b时,函数y=f(x)在定义域[a,b]上的最小值为0,根据值域是
 ,
,可得
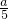 =0,a=0 (不合题意舍去).
=0,a=0 (不合题意舍去).综上,存在a=
 ,b=
,b= 满足条件.
满足条件.分析:(1)根据条件可得1-
 =-(1-
=-(1- ),即2=
),即2= +
+ ,利用基本不等式可得
,利用基本不等式可得 <1,从而得到ab>1.
<1,从而得到ab>1.(2)当1≤a<b 时,可得
 =1-
=1- 在[a,b]上是增函数,故有 1-
在[a,b]上是增函数,故有 1- =
= a,1-
a,1- =
= b,解出a、b的值.
b,解出a、b的值.当0<a<b≤1时,可得
 =
= -1 在[a,b]上是减函数,故有
-1 在[a,b]上是减函数,故有 =
= ,
, =
= ,解得a、b 无解.
,解得a、b 无解.当0<a<1<b时,函数y=f(x)在定义域[a,b]上的最小值为0,根据值域是
 ,解得a、b 无解.
,解得a、b 无解.点评:本题主要考查求函数的定义域、值域,带绝对值的函数,体现了分类讨论的数学思想.

练习册系列答案
相关题目
 .
. .
. .
. .
.