题目内容
(14分)
设函数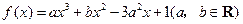 在
在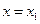 ,
,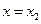 处取得极值,且
处取得极值,且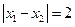 .
.
(Ⅰ)若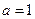 ,求
,求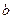 的值,并求
的值,并求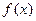 的单调区间;
的单调区间;
(Ⅱ)若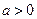 ,求
,求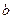 的取值范围.
的取值范围.

(Ⅱ)由①式及题意知 为方程
为方程 的两根,
的两根,
所以 .从而
.从而 ,
,
由上式及题设知 .························· 8分
.························· 8分
考虑 ,
, . ………………………10分
. ………………………10分
故 在
在 单调递增,在
单调递增,在 单调递减,从而
单调递减,从而 在
在 的极大值为
的极大值为
 .
.
又 在
在 上只有一个极值,所以
上只有一个极值,所以 为
为 在
在 上的最大值,且最小值为
上的最大值,且最小值为 ………………………………12分
………………………………12分
所以 ,即
,即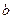 的取值范围为
的取值范围为 ………………14分
………………14分
法二:
由①式及题意知 为方程
为方程 的两根,
的两根,
所以 .从而
.从而 ,
,
由上式及题设知 . ……………………………8分
. ……………………………8分
所以 ,即
,即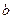 的取值范围为
的取值范围为 ………………14分
………………14分
解析

练习册系列答案
相关题目
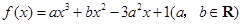 在
在 ,
,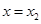 处取得极值,且
处取得极值,且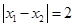 .
.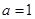 ,求
,求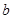 的值,并求
的值,并求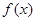 的单调区间;
的单调区间;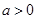 ,求
,求