题目内容
已知数列{an}的前n项和Sn与通项an之间满足关系Sn= -
-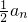
(I)求数列{an}的通项公式;
(II)设f(x)=log3x,bn=f(a1)+f(a2)+L+f(an),Tn= ,求T2012
,求T2012
(III)若cn=an•f(an),求{cn}的前n项和an.
解:(I)n=1时,a1=S1= -
- a1,∴a1=
a1,∴a1= (1分)
(1分)
n≥2时,an=Sn-Sn-1= -
-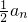 -
- +
+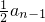 ,∴an=
,∴an= an-1,
an-1,
即数列{an}是首项为 ,公比为
,公比为 的等比数列 (3分)
的等比数列 (3分)
故an= (4分)
(4分)
(II)由已知可得:f(an)=-n,则bn=f(a1)+f(a2)+…+f(an)=-1-2-…-n=- (5分)
(5分)
∴
 ) (6分)
) (6分)
∴Tn= =2[(1-
=2[(1- )+(
)+( )+…+(
)+…+( )]=-2(1-
)]=-2(1- )
)
∴T2012=- (8分)
(8分)
(III)由题意:cn=an•f(an)=-n× ,故{cn}的前n项和un=-[1×
,故{cn}的前n项和un=-[1× +2×
+2× +…+n×
+…+n× ]①
]①
∴ un=-[1×
un=-[1× +2×
+2× +…+n×
+…+n× ]②
]②
①-②可得: un=-[
un=-[ +
+ +
+ +…+
+…+ -n×
-n× ](12分)
](12分)
∴ un=-
un=- [1-
[1- ]+n×
]+n×
∴un=- +
+ ×
× +
+ n×
n× (14分)
(14分)
分析:(I)n=1时,a1=S1,n≥2时,an=Sn-Sn-1,由此可得数列{an}是首项为 ,公比为
,公比为 的等比数列,故可求数列{an}的通项公式;
的等比数列,故可求数列{an}的通项公式;
(II)由已知可得:f(an)=-n,则bn=- ,所以
,所以
 ),利用叠加法可求T2012的值;
),利用叠加法可求T2012的值;
(III)由题意:cn=an•f(an)=-n× ,利用错位相减法可求{cn}的前n项和.
,利用错位相减法可求{cn}的前n项和.
点评:本题考查数列递推式,考查等比数列的证明,考查数列的通项与求和,确定数列的通项,掌握求和的方法是关键.
 -
- a1,∴a1=
a1,∴a1= (1分)
(1分)n≥2时,an=Sn-Sn-1=
 -
-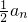 -
- +
+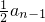 ,∴an=
,∴an= an-1,
an-1,即数列{an}是首项为
 ,公比为
,公比为 的等比数列 (3分)
的等比数列 (3分)故an=
 (4分)
(4分)(II)由已知可得:f(an)=-n,则bn=f(a1)+f(a2)+…+f(an)=-1-2-…-n=-
 (5分)
(5分)∴

 ) (6分)
) (6分)∴Tn=
 =2[(1-
=2[(1- )+(
)+( )+…+(
)+…+( )]=-2(1-
)]=-2(1- )
)∴T2012=-
 (8分)
(8分)(III)由题意:cn=an•f(an)=-n×
 ,故{cn}的前n项和un=-[1×
,故{cn}的前n项和un=-[1× +2×
+2× +…+n×
+…+n× ]①
]①∴
 un=-[1×
un=-[1× +2×
+2× +…+n×
+…+n× ]②
]②①-②可得:
 un=-[
un=-[ +
+ +
+ +…+
+…+ -n×
-n× ](12分)
](12分)∴
 un=-
un=- [1-
[1- ]+n×
]+n×
∴un=-
 +
+ ×
× +
+ n×
n× (14分)
(14分)分析:(I)n=1时,a1=S1,n≥2时,an=Sn-Sn-1,由此可得数列{an}是首项为
 ,公比为
,公比为 的等比数列,故可求数列{an}的通项公式;
的等比数列,故可求数列{an}的通项公式;(II)由已知可得:f(an)=-n,则bn=-
 ,所以
,所以
 ),利用叠加法可求T2012的值;
),利用叠加法可求T2012的值;(III)由题意:cn=an•f(an)=-n×
 ,利用错位相减法可求{cn}的前n项和.
,利用错位相减法可求{cn}的前n项和.点评:本题考查数列递推式,考查等比数列的证明,考查数列的通项与求和,确定数列的通项,掌握求和的方法是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |