题目内容
若 ,定义一种向量积:
,定义一种向量积: ,
,
已知 ,且点
,且点 在函数
在函数 的图象上运动,点
的图象上运动,点 在函数
在函数 的图象上运动,且点
的图象上运动,且点 和点
和点 满足:
满足: (其中O为坐标原点),则函数
(其中O为坐标原点),则函数 的最大值
的最大值 及最小正周期
及最小正周期 分别为
分别为
A. | B. | C. | D. |
D
解析试题分析:由题意可知 =(x,sinx),
=(x,sinx), ,
,
根据新定义可知 =(2x,
=(2x,
 )+(
)+( ,0)=(2x+
,0)=(2x+ ,
,
 )
)
而点Q在y=f(x)的图象上运动
∴f(2x+ )=
)=

则f(x)=

∴y=f(x)的最大值、周期分别为 ,
,
故选D.
考点:本题主要考查平面向量的坐标运算,三角函数的图象和性质。
点评:新定义问题,此类题目往往作为“创新题”出现,关键是读懂题意,明确新定义运算方法及结果。

练习册系列答案
相关题目
设 ,向量
,向量 且
且 ,则
,则 ( )
( )
A. | B. | C.2 | D.10 |
已知△ABC和点M满足 .若存在实数m使得
.若存在实数m使得 成立,则m=( )
成立,则m=( )
| A.2 | B.3 | C.4 | D.5 |
若 是非零向量且满足
是非零向量且满足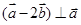 ,
, ,则
,则 与
与 的夹角是( )
的夹角是( )
A. | B. | C. | D. |
已知 =(5,-3),C(-1,3),
=(5,-3),C(-1,3), =2
=2 ,则点D的坐标为
,则点D的坐标为
| A.(11,9) | B.(4,0) | C.(9, 3) | D.(9,-3) |
在空间四边形 中,
中, ,
, ,
, ,
, ,
, 分别为
分别为 、
、 的中点,则
的中点,则 可表示为( )
可表示为( )
A. | B. |
C. | D. |
已知向量 且
且 ,则实数x等于 ( )
,则实数x等于 ( )
A. | B. 9 | C. 4 | D. -4 |
 =( )
=( )
| A.1 | B.4 | C.2 | D.8 |
设 是单位向量,且
是单位向量,且 ,则
,则
 (
( -
- )的最小值为( )
)的最小值为( )
A. | B. | C. | D. |