题目内容
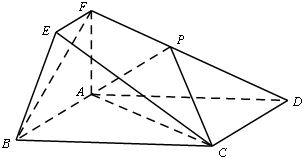 (2012•丰台区二模)在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2EF=1,点P在棱DF上.
(2012•丰台区二模)在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2EF=1,点P在棱DF上.(Ⅰ)若P是DF的中点,
(ⅰ) 求证:BF∥平面ACP;
(ⅱ) 求异面直线BE与CP所成角的余弦值;
(Ⅱ)若二面角D-AP-C的余弦值为
| ||
| 3 |
分析:(Ⅰ)(ⅰ)连接BD,交AC于点O,连接OP.利用OP为三角形BDF中位线,可得BF∥OP,利用线面平行的判定,可得BF∥平面ACP;
(ⅱ)利用平面ABEF⊥平面ABCD,可得⊥平面ABCD,建立空间直角坐标系,求得
=(-
,0,1),
=(-1,-1,
),利用向量的夹角公式,即可求异面直线BE与CP所成角的余弦值;
(Ⅱ)设P点坐标为(0,2-2t,t),求得平面APF的法向量为
=(1,0,0),平面APC的法向量为
=(-2,1,
),利用向量的夹角公式,即可求得结论.
(ⅱ)利用平面ABEF⊥平面ABCD,可得⊥平面ABCD,建立空间直角坐标系,求得
| BE |
| 1 |
| 2 |
| CP |
| 1 |
| 2 |
(Ⅱ)设P点坐标为(0,2-2t,t),求得平面APF的法向量为
| n1 |
| n2 |
| 2t-2 |
| t |
解答:(Ⅰ)(ⅰ)证明:连接BD,交AC于点O,连接OP.
因为P是DF中点,O为矩形ABCD 对角线的交点,所以OP为三角形BDF中位线,所以BF∥OP,
因为BF?平面ACP,OP?平面ACP,所以BF∥平面ACP. …(4分)
(ⅱ)因为∠BAF=90°,所以AF⊥AB,
因为平面ABEF⊥平面ABCD,且平面ABEF∩平面ABCD=AB,所以AF⊥平面ABCD,
因为四边形ABCD为矩形,所以以A为坐标原点,AB,AD,AF分别为x,y,z轴,建立如图所示空间直角坐标系O-xyz.
所以B(1,0,0),E(
,0,1),P(0,1,
),C(1,2,0).
所以
=(-
,0,1),
=(-1,-1,
),
所以cos<
,
>=
=
,
即异面直线BE与CP所成角的余弦值为
. …(9分)
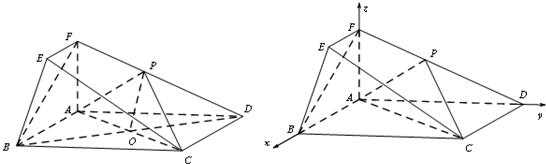
(Ⅱ)解:因为AB⊥平面ADF,所以平面APF的法向量为
=(1,0,0).
设P点坐标为(0,2-2t,t),在平面APC中,
=(0,2-2t,t),
=(1,2,0),
所以平面APC的法向量为
=(-2,1,
),
所以cos<
,
>=
=
=
,
解得t=
,或t=2(舍).
此时|PF|=
. …(14分)
因为P是DF中点,O为矩形ABCD 对角线的交点,所以OP为三角形BDF中位线,所以BF∥OP,
因为BF?平面ACP,OP?平面ACP,所以BF∥平面ACP. …(4分)
(ⅱ)因为∠BAF=90°,所以AF⊥AB,
因为平面ABEF⊥平面ABCD,且平面ABEF∩平面ABCD=AB,所以AF⊥平面ABCD,
因为四边形ABCD为矩形,所以以A为坐标原点,AB,AD,AF分别为x,y,z轴,建立如图所示空间直角坐标系O-xyz.
所以B(1,0,0),E(
| 1 |
| 2 |
| 1 |
| 2 |
所以
| BE |
| 1 |
| 2 |
| CP |
| 1 |
| 2 |
所以cos<
| BE |
| CP |
| ||||
|
4
| ||
| 15 |
即异面直线BE与CP所成角的余弦值为
4
| ||
| 15 |

(Ⅱ)解:因为AB⊥平面ADF,所以平面APF的法向量为
| n1 |
设P点坐标为(0,2-2t,t),在平面APC中,
| AP |
| AC |
所以平面APC的法向量为
| n2 |
| 2t-2 |
| t |
所以cos<
| n1 |
| n2 |
|
| ||||
|
|
| 2 | ||||
|
| ||
| 3 |
解得t=
| 2 |
| 3 |
此时|PF|=
| ||
| 3 |
点评:本题考查线面平行,考查线线角、面面角,考查利用空间向量解决空间角问题,正确求向量是关键.

练习册系列答案
相关题目
 (2012•丰台区二模)执行如图所示的程序框图,若输出的结果为63,则判断框中应填( )
(2012•丰台区二模)执行如图所示的程序框图,若输出的结果为63,则判断框中应填( ) (2012•丰台区二模)如图所示,四棱锥P-ABCD中,底面ABCD是边长为2的菱形,Q是棱PA上的动点.
(2012•丰台区二模)如图所示,四棱锥P-ABCD中,底面ABCD是边长为2的菱形,Q是棱PA上的动点.