题目内容
(本小题满分12分)
已知函数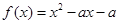 ,
,
(1)
若存在实数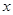 ,使得
,使得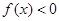 ,求实数
,求实数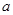 的取值范围;
的取值范围;
(2)
设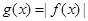 ,且
,且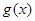 在区间
在区间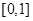 上单调递增,求实数
上单调递增,求实数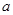 的取值范围。
的取值范围。
【答案】
(1)存在实数 或
或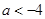 ;(2)
;(2)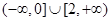 。
。
【解析】
试题分析:(1)直接零函数小于零,解一元二次不等式即可
(2)根据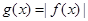 ,且
,且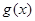 在区间
在区间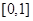 上单调递增,那么可知对于参数a进行分类讨论得到结论。
上单调递增,那么可知对于参数a进行分类讨论得到结论。
解:(1)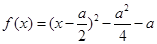 ,当仅当
,当仅当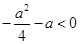 时,存在实数
时,存在实数 或
或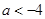 …………………3分
…………………3分
(2)当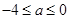 时,
时,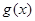 在
在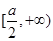 上递增,则
上递增,则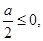 即
即 …………………5分
…………………5分
当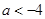 或
或 时,设
时,设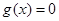 的两根为
的两根为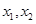 ,且
,且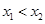 ,此时
,此时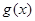 在区间
在区间 或
或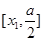 上递增。…………………7分。
上递增。…………………7分。
若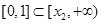 ,则
,则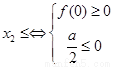 ,得
,得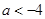 ;…………………9分
;…………………9分
若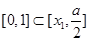 ,则
,则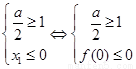 ,得
,得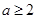 ,…………………11分
,…………………11分
综上可知,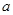 的取值范围是
的取值范围是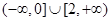 …………………12分。
…………………12分。
考点:本试题主要考查了一元二次不等式的求解以及函数单调性的运用。
点评:解决该试题的关键是根据已知条件得到二次不等式,结合二次函数性质得到结论。同时对于绝对值函数,要分类去掉其符号。

练习册系列答案
相关题目