Question

已知函数y=x²＋(2m＋1)x＋m²－1(m∈R).

(1)m为何值时，y的极小值是0？

(2)求证：不论m是什么数值，函数的图象(即抛物线)的顶点都在同一条直线l₁上.

(3)平行于l₁的直线中，哪些与抛物线相交，哪些不相交？求证：任一条平行于l₁而与抛物线相交的直线，被各抛物线截出的线段都相等.

Answer 1

(1)解:用配方法得y=(x＋)²－，

∴y的极小值为－.

由－=0，得m=－,即当m=－时，y的极小值是0.

(2)证明:函数图象抛物线的顶点坐标为(－，－),

即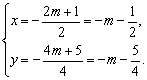(x、y为顶点的两坐标)

两式相减得x－y=，此即各抛物线顶点坐标所满足的方程，它的图形是一条直线.方程中不含m，因此，不论m是什么值,抛物线的顶点都在这条直线l₁:x－y=上.

(3)设l:x－y=a为任一条平行于l₁的直线,

由

消去y，得x²＋2mx＋m²－1＋a=0，即(x＋m)²=1－a.

当1－a≥0，即a≤1时，直线l与抛物线相交，而1－a＜0，即a＞1时，直线l与抛物线不相交.

若a≤1，则x=－m±,即x₁=－m－，x₂=－m＋.

∴x₂－x₁=2.

直线l被抛物线截得的线段AB的长为

|AB|=|x₂－x₁|=·2=2与m无关.

因而直线l被各抛物线截出的线段都相等.