题目内容
10.已知数列{an}的通项公式an=-n2+13n-$\frac{133}{4}$.当a1a2a3+a2a3a4+a3a4a5+…+anan+1an+2取得最大值时,n的值为9.分析 通过配方可知该数列当从第4项至第9项为正数、其余项为负数,进而计算可得结论.
解答 解:∵an=-n2+13n-$\frac{133}{4}$=-(n-$\frac{13}{2}$)2+9,
∴an>0,等价于$\frac{7}{2}$<n<$\frac{19}{2}$,
∴当从第4项至第9项为正数,其余项为负数,
∴当n>11时,anan+1an+2恒小于0,
又∵a9a10a11>0>a8a9a10,
∴a1a2a3+a2a3a4+a3a4a5+…+anan+1an+2取得最大值时n=9,
故答案为:9.
点评 本题考查数列的前n项的若干项乘积之和取最大值时项数n的求法,解题时要认真审题,注意数列中各项符号的合理运用,属于中档题.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
2.不等式x2-x-2≥0和x2-(2a+1)x+a2+a>0的解集分别为A和B,且A⊆B,则实数a取值范围是( )
| A. | (0,1) | B. | [0,1] | C. | [-1,1] | D. | (-1,1) |
15.已知$\left\{\begin{array}{l}{-2x+y≤2}\\{x-2y≤2}\\{x+y≤5}\\{x≥0,y≥0}\end{array}\right.$,则-x+y的最大值是3.
18.下列函数是奇函数的是( )
| A. | f(x)=x|x| | B. | f(x)=lgx | C. | f(x)=2x+2-x | D. | f(x)=x3-1 |
 .
.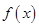 最小正周期;
最小正周期;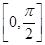 上的最大值和最小值.
上的最大值和最小值.