题目内容
在等差数列{an}中,若a1004+a1006+a1008=6,则该数列的前2011项的和为( )A.4022
B.4020
C.2011
D.2010
【答案】分析:利用等差中项的性质根据a1004+a1006+a1008=3,求得a1006,代入到前2011项的和中求得答案.
解答:解:∵a1004+a1006+a1008=6得
∴3a1006=6,a1006=2
∴Sn=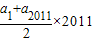 =4022,
=4022,
故选A.
点评:本题主要考查了等差数列的前n项的和.若直接用通项公式和求和公式求解较复杂,解答中应用等差数列的性质am+an=ap+aq,结论巧妙产生,过程简捷,运算简单.
解答:解:∵a1004+a1006+a1008=6得
∴3a1006=6,a1006=2
∴Sn=
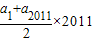 =4022,
=4022,故选A.
点评:本题主要考查了等差数列的前n项的和.若直接用通项公式和求和公式求解较复杂,解答中应用等差数列的性质am+an=ap+aq,结论巧妙产生,过程简捷,运算简单.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目