题目内容
用0到9这10个数字，可以组成没有重复数字的三位偶数的个数为( )
| A．324 | B．328 | C．360 | D．648 |
B
解析试题分析：如果0在末位，则有
个符合要求的数；如果0不在末位，则末位有2，4，6，8四种选择，首位有8种选择，所以有
个符合要求的数，所以共有
个符合要求的数.
考点：本小题主要考查两个计数原理和排列组合的应用.
点评：本小题主要用到的方法是特殊位置优先法，要注意排列组合中特定方法的灵活应用.
练习册系列答案
小学教材全测系列答案
相关题目
从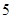
位男数学教师和
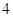位女数学教师中选出
位教师派到个班担任班主任（每班
位班主任），要求这位班主任中男女教师都有，则不同的选派方案共有（ ）
| A．210 | B．420 | C．630 | D．840 |
数学中无论从左往右读，还是从右往左读，都是同一个数，称这样的数为“回文数”，如： 88，454，7337，43534等都是回文数，体现对称美，读起来还真有趣！那么六位的回文数共有( )个.
| A．800 | B．810 | C．900 | D．1000 |
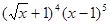的展开式中，
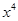的系数为（ ）
| A．－40 | B．10 | C．40 | D．45 |
从5名志愿者中选派4人在星期五、星期六、星期日参加公益活动，每人一天，要求星期五有一人参加，星期六有两人参加，星期日有一人参加，则不同的选派方法共有（ ）
| A．120种 | B．96种 | C．60种 | D．48种 |
用二项式定理计算9.985，精确到1的近似值为 ( )
| A．99000 | B．99002 | C．99004 | D．99005 |
2013年第12届全国运动会举行期间，某校4名大学生申请当A，B，C三个比赛项目的志愿者，组委会接受了他们的申请，每个比赛项目至少分配一人，每人只能服务一个比赛项目，若甲要求不去服务A比赛项目，则不同的安排方案共有（ ）
| A．20种 | B．24种 | C．30种 | D．36种 |
两位同学一起去一家单位应聘，面试前单位负责人对他们说：“我们要从面试的人中招聘3人，你们俩同时被招聘进来的概率是1∕70”．根据这位负责人的话可以推断出参加面试的人数为（ ）
| A．21 | B．35 | C．42 | D．70 |
现有高一年级的学生
名，高二年级的学生
名，高三年级的学生
名，从中任选
人参加某项活动，则不同选法种数为（ ）
| A．60 | B．12 | C．5 | D．5 |