题目内容
若函数
在
处取得极值．
(1) 求a的值；
(2) 求函数
的单调区间．
解：(1)f′(x)＝2ax＋2－
，
由f′(1)＝2a＋
＝0，得a＝－
.
(2)f(x)＝－x2＋2x－
lnx(x>0)．
f′(x)＝－x＋2－＝
由f′(x)＝0，得x＝1或x＝2.
①当f′(x)>0时1<x<2；
②当f′(x)<0时0<x<1或x>2.
当x变化时f′(x)，f(x)的变化情况如下：
| x | (0,1) | 1 | (1,2) | 2 | (2，＋∞) |
| f′(x) | － | 0 | ＋ | 0 | － |
| f(x) | ↘ |
| ↗ |
| ↘ |
－
练习册系列答案
相关题目
的图像与
轴恰好有三个不同的公共点，则实数
的取值范围是（ ）
是R上的函数，当
时，
，若
，则
的大小关系是（ ）
B.
C.
D.
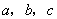中恰有一个偶数”正确的反设
的单调递减区间为 ．
,并且a是第二象限的角,那么tana的值等于 （ ）
B.- 
C. 
|=- cos
在区间
的值域为
B．
C．
D．
D．e2—2e+1