Question

已知不等式ax²+bx+c＞0的解集为(α,β)，且0＜α＜β,求不等式cx²+bx+a＜0的解集.

Answer 1

答案：解法一：由已知不等式可得a＜0,且α,β为方程ax²+bx+c=0的两根，∴由韦达定理可得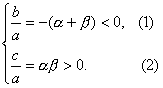

∵a＜0,∴由②得c＜0,则cx²+bx+a＜0可化为x²+x+＞0，

①÷②，得==-(+)＜0.

由②得==·＞0.

∴,为x²+x+＞0的两根.

又0＜α＜β,0＜＜，∴不等式x²+x+＞0的解集为{x|x＜或x＞}，

即不等式cx²+bx+a＜0的解集为{x|x＜或x＞}.

解法二：∵a＜0，由cx²+bx+a＜0,得x²+x+1＞0，

将①②代入，得αβx²-(α+β)x+1＞0，即(αx-1)(βx-1)＞0.

又0＜α＜β， ∴0＜＜.

∴所求不等式的解集为{x|x＜或x＞}.