题目内容
下列函数中既是奇函数,又在区间(0,+∞)上单调递增的是
- A.y=-x2
- B.
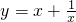
- C.y=1g(2x)
- D.y=e|x|
C
分析:作为选择题可选用排除法,如A,D是偶函数,B,可用具体验证不是单调函数,自然就选C了.
解答:A、D、都满足f(-x)=f(x)是偶函数,
B、f(-x)=-( )=-f(x),是奇函数,∵f(2)=f(
)=-f(x),是奇函数,∵f(2)=f( )∴在(0,+∝)上不单调.
)∴在(0,+∝)上不单调.
C、f(-x)=lg(2-x)=lg((2x)-1)=-f(x)是奇函数.
令t=2x,y=lgt,因为两个函数在定义域上都是增函数,由复合函数单调性可知,函数在定义域上是增函数.
故选C
点评:本题主要考查函数奇偶性和单调性的判断,判断单调性可用多种方法,证明时只能用单调性定义和导数法.
分析:作为选择题可选用排除法,如A,D是偶函数,B,可用具体验证不是单调函数,自然就选C了.
解答:A、D、都满足f(-x)=f(x)是偶函数,
B、f(-x)=-(
 )=-f(x),是奇函数,∵f(2)=f(
)=-f(x),是奇函数,∵f(2)=f( )∴在(0,+∝)上不单调.
)∴在(0,+∝)上不单调.C、f(-x)=lg(2-x)=lg((2x)-1)=-f(x)是奇函数.
令t=2x,y=lgt,因为两个函数在定义域上都是增函数,由复合函数单调性可知,函数在定义域上是增函数.
故选C
点评:本题主要考查函数奇偶性和单调性的判断,判断单调性可用多种方法,证明时只能用单调性定义和导数法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f(x)=
,那么下列函数中既是奇函数又是周期函数的是( )
|
| A、y=f(x)sinx |
| B、y=f(x)+sinx |
| C、y=sin[f(x)] |
| D、y=f(sinx) |