题目内容
设函数 ,其中
,其中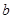 为常数。
为常数。
(Ⅰ)当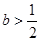 时,判断函数
时,判断函数 在定义域上的单调性;
在定义域上的单调性;
(Ⅱ)若函数 有极值点,求
有极值点,求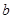 的取值范围及
的取值范围及 的极值点。
的极值点。
(Ⅰ)函数 在定义域
在定义域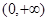 上单调递增;(Ⅱ)当且仅当
上单调递增;(Ⅱ)当且仅当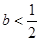 时
时 有极值点; 当
有极值点; 当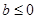 时,
时, 有惟一最小值点
有惟一最小值点 ;当
;当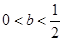 时,
时, 有一个极大值点
有一个极大值点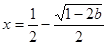 和一个极小值点
和一个极小值点 .
.
解析试题分析:(Ⅰ)函数 在定义域上的单调性的方法,一是利用定义,二是利用导数,此题既有代数函数又有对数函数,显然利用导数判断,只需对
在定义域上的单调性的方法,一是利用定义,二是利用导数,此题既有代数函数又有对数函数,显然利用导数判断,只需对 求导,判断
求导,判断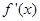 的符号即可;(Ⅱ)求
的符号即可;(Ⅱ)求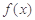 的极值,只需对
的极值,只需对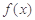 求导即可,利用导数求函数的极值一般分为四个步骤:①确定函数的定义域;②求出
求导即可,利用导数求函数的极值一般分为四个步骤:①确定函数的定义域;②求出 ;③令
;③令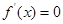 ,列表;④确定函数的极值.此题由(Ⅰ)得,当
,列表;④确定函数的极值.此题由(Ⅰ)得,当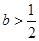 时,函数
时,函数 无极值点,只需讨论
无极值点,只需讨论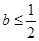 的情况,解
的情况,解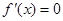 的根,讨论在
的根,讨论在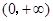 范围内根的个数,从而确定
范围内根的个数,从而确定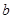 的取值范围及
的取值范围及 的极值点,值得注意的是,求出
的极值点,值得注意的是,求出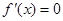 的根时,忽略讨论根是否在定义域内,而出错.
的根时,忽略讨论根是否在定义域内,而出错.
试题解析:(Ⅰ)由题意知, 的定义域为
的定义域为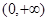 ,
,
 ∴当
∴当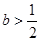 时,
时,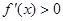 ,函数
,函数 在定义域
在定义域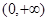 上单调递增.
上单调递增.
(Ⅱ)①由(Ⅰ)得,当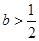 时,函数
时,函数 无极值点,②
无极值点,② 时,
时,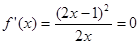 有两个相同的解
有两个相同的解 ,但当
,但当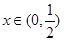 时,
时,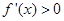 ,当
,当 时,
时,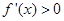
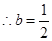 时,函数
时,函数 在
在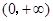 上无极值点,③当
上无极值点,③当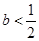 时,
时,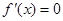 有两个不同解,
有两个不同解,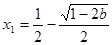
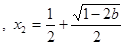 ,
,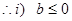 时,
时, ,而
,而 ,此时
,此时 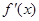 ,
, 随
随 在定义域上的变化情况如下表:
在定义域上的变化情况如下表:
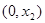
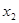
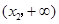
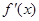


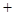

减 
学而优中考专题分类集训南京大学出版社系列答案
浙大优学中考探究题精析精练系列答案
励耘第二卷三年中考优化卷系列答案
中考必备中考真题精编系列答案
四川高考一轮复习导学案系列答案
经纶学典默写达人系列答案
名师讲坛1课1练系列答案
名师导航同步练与测系列答案
课堂感悟系列答案
经纶学典中考分类精华集系列答案
 。
。 时,求函数
时,求函数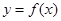 的单调区间;
的单调区间;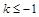 时,对所有的
时,对所有的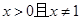 都有
都有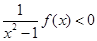 成立.
成立.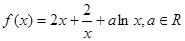 .
. 在
在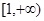 上单调递增,求实数
上单调递增,求实数 的取值范围.
的取值范围.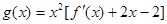 ,若
,若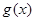 的最小值是
的最小值是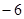 ,求函数
,求函数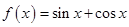 ,
,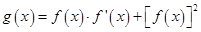
 的周期和对称中心;
的周期和对称中心;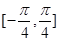 上值域.
上值域. 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛 ,要求
,要求 在
在 的延长线上,
的延长线上, 在
在 的延长线上,且对角线
的延长线上,且对角线 过
过 点.已知
点.已知 米,
米, 米。
米。
 (单位:米),要使花坛
(单位:米),要使花坛 的取值范围;
的取值范围;  (单位:米),则当
(单位:米),则当 ,
, 的长度分别是多少时,花坛
的长度分别是多少时,花坛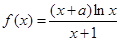 ,曲线
,曲线 在点
在点 处的切线与直线
处的切线与直线 垂直.
垂直. 的值;
的值;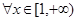 ,
,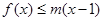 恒成立,求
恒成立,求 的范围.
的范围.
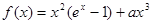
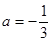 时,求
时,求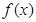 的单调区间;
的单调区间;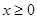 时,
时,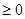 恒成立,求
恒成立,求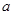 的取值范围.
的取值范围.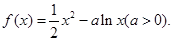
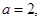 求
求 在
在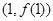 处的切线方程;
处的切线方程; 上恰有两个零点,求
上恰有两个零点,求 的取值范围.
的取值范围. 是实数,函数
是实数,函数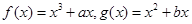 ,
, 和
和 ,分别是
,分别是 的导函数,若
的导函数,若 在区间
在区间 上恒成立,则称
上恒成立,则称 和
和 在区间
在区间 ,若函数
,若函数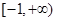 上单调性一致,求实数
上单调性一致,求实数 的取值范围;
的取值范围; 且
且 ,若函数
,若函数 的最大值.
的最大值.