题目内容

（本小题满分10分）已知函数()  

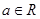（1）求函数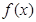的极大值和极小值；

（2）若函数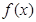在区间[－2，2]上的最大值为20，求它在该区间上的最小值。

 

【答案】

（1）

 

x

-1

(-1,3)

3

-

0

+

0

-

极小值

-5+a

极大值

27+ a

 

 

【解析】本试题主要是考查而来导数在研究函数中的运用求解极值和最值问题。

（1）因为函数，求解导数，根据导数的符号与函数单调性的关系，判定单调性得到极值。

（2）在第一问的基础上分析最值，并得到最小值。

解：

（1）令得或

的单调递减区间为

 

x

-1

(-1,3)

3

-

0

+

0

-

极小值

-5+a

极大值

27+ a

 

 

练习册系列答案
相关题目
（选做题）本题包括A、B、C、D四小题，请选定其中两题，并在答题卡指定区域内作答，若多做，则按作答的前两题评分，解答时应写出文字说明、证明过程或演算步骤．
A．[选修4-1：几何证明选讲]
已知△ABC中，AB=AC，D是△ABC外接圆劣弧AC上的点（不与点A，C重合），延长BD至点E．
求证：AD的延长线平分∠CDE
B．[选修4-2：矩阵与变换]
已知矩阵A=
12
-14

（1）求A的逆矩阵A-1；
（2）求A的特征值和特征向量．
C．[选修4-4：坐标系与参数方程]
已知曲线C的极坐标方程为ρ=4sinθ，以极点为原点，极轴为x轴的非负半轴建立平面直角坐标系，直线l的参数方程为
x=
1
2
t
y=
3
2
t+1
（t为参数），求直线l被曲线C截得的线段长度．
D．[选修4-5，不等式选讲]（本小题满分10分）
设a，b，c均为正实数，求证：
1
2a
+
1
2b
+
1
2c
≥
1
b+c
+
1
c+a
+
1
a+b
．
本题包括（1）、（2）、（3）、（4）四小题，请选定其中两题，并在答题卡指定区域内答，
若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．
（1）、选修4-1：几何证明选讲
如图，∠PAQ是直角，圆O与AP相切于点T，与AQ相交于两点B，C．求证：BT平分∠OBA
（2）选修4-2：矩阵与变换（本小题满分10分）
若点A（2，2）在矩阵M=
cosα-sinα
sinαcosα
对应变换的作用下得到的点为B（-2，2），求矩阵M的逆矩阵
（3）选修4-2：矩阵与变换（本小题满分10分）
在极坐标系中，A为曲线ρ2+2ρcosθ-3=0上的动点，B为直线ρcosθ+ρsinθ-7=0上的动点，求AB的最小值．
（4）选修4-5：不等式选讲（本小题满分10分）
已知a1，a2…an都是正数，且a1•a2…an=1，求证：（2+a1）（2+a2）…（2+an）≥3n．
必做题：（本小题满分10分，请在答题指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
已知an（n∈N*）是二项式（2+x）n的展开式中x的一次项的系数．
（Ⅰ）求an；
（Ⅱ）是否存在等差数列{bn}，使an=b1cn1+b2cn2+b3cn3+…+bncnn对一切正整数n都成立？并证明你的结论．
（本小题满分10分）数学的美是令人惊异的！如三位数153，它满足153=13+53+33，即这个整数等于它各位上的数字的立方的和，我们称这样的数为“水仙花数”．请您设计一个算法，找出大于100，小于1000的所有“水仙花数”．
（1）用自然语言写出算法；
（2）画出流程图．
（选修4-2：矩阵与变换）（本小题满分10分）
求矩阵A=
32
21
的逆矩阵．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网