Question

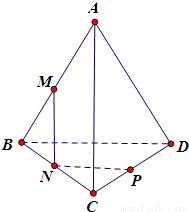
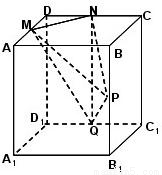
如图，M、N、P分别是正方体的棱AB、BC、DD₁上的点．
（1）若

BM

MA

=

BN

NC

，求证：无论点P在D₁D上如何移动，总有BP⊥MN；
（2）若D₁P：PD=1：2，且PB⊥平面B₁MN，求二面角M-B₁N-B的大小．

Answer 1

分析：（1））证法一：连AC、BD，则BD⊥AC，通过

BM

MA

=

BN

NC

，证明MN⊥平面BDD₁．总有MN⊥BP．
证法二：连接AC、BD，则AC⊥BD．利用

BM

MA

=

BN

NC

，证明MN⊥PB．可得总有BP⊥MN；
（2）解法一：过P作PG⊥C₁C交CC₁于G，连BG交B₁N于O₁，说明∠MO₁B就是二面角M-B₁N-B的平面角，利用△MO₁B求解即可．
解法二：设BD与MN相交于F，连接B₁F，设二面角B-B₁N-M的平面角为α，则cosα=

S△B1BN

S△B1MN

，求解即可．

解答：解：（1）证法一：连AC、BD，则BD⊥AC，
∵

BM

MA

=

BN

NC

，∴MN∥AC，∴BD⊥MN．
又∵DD₁⊥平面ABCD，∴DD₁⊥MN，
∴MN⊥平面BDD₁．
∵无论点P在DD₁上如何移动，总有BP?平面BDD₁，
故总有MN⊥BP．
证法二：连接AC、BD，则AC⊥BD．
∵

BM

MA

=

BN

NC

，∴MN∥AC，∴MN⊥BD，又PD⊥平面ABCD，
由三垂线定理得：MN⊥PB．
（2）解法一：过P作PG⊥C₁C交CC₁于G，连BG交B₁N于O₁，
∵PB⊥平面B₁MN，∴PB⊥B₁N．
又∵PG⊥平面B₁BCC₁，∴BG⊥B₁N，∴△BB₁N≌△BCG，∴BN=CG，NC=GC₁，
∴BN：NC=DP：PD₁=2：1．
同理BM：MA=DP：PD₁=2：1．
设AB=3a，则BN=2a，∴B1N=

9a2+4a2

=

13

a，
BO1=

BN•BB1

B1N

=

3a•2a

13 a

=

6a

13

，
连MO₁，∵AB⊥平面B₁BCC₁，∴MO₁⊥B₁N，
∵∠MO₁B就是二面角M-B₁N-B的平面角，
tan∠MO1B=

BM

BO1

=

2a

6a 13

=

13

3

，
∴∠MO1B=arctan 

13

3

．
解法二：设BD与MN相交于F，连接B₁F，
∵PB⊥平面MNB₁，∴PB⊥B₁F，PB⊥MN，
∴在对角面BB₁D₁D内，△PBD∽△BB₁F，
设BB₁=DD₁=3，则PD=2，BD=3

2

，∴

BF

PD

=

BB1

BD

，即

BF

2

=

3

3 2

，故BF=

2

．
∵MN⊥PB，由三垂线定理得MN⊥BD，MN∥AC，MN=2BF=2

2

，BN=2，
B1F=

B1B2+BF2

=

32+22

=11．
设二面角B-B₁N-M的平面角为α，则cosα=

S△B1BN

S△B1MN

=

1 2 ×2×3

1 2 ×2 2 × 11

=

3

22

=

3 22

22

，
α=arccos

3 22

22

．

点评：本题是中档题，考查直线与直线的垂直的证明方法，二面角的求法，考查空间想象能力，计算能力．