题目内容

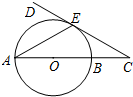（2013•永州一模）如图，AB是⊙O的直径，C是AB延长线上一点，CD与⊙O相切于点E，∠C=
π
6
，则∠AED=
π
3
π
3
．
分析：如图所示，连接OE．利用切线的性质及CD与⊙O相切于点E，可得OE⊥CD．即可得出∠COE，由OE=OA，可得∠OEA即可．
解答：解：如图所示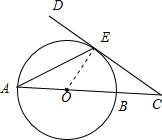，连接OE．∵CD与⊙O相切于点E，∴OE⊥CD．
∵∠C=
π
6
，∴∠COE=
π
3
．
∵OA=OE，∴∠OAE=∠OEA=
π
6
．
∴∠AED=∠ODE-∠OEA=
π
3
．
故答案为
π
3
．
点评：熟练掌握圆的切线的性质、圆的性质是解题的关键．
练习册系列答案
相关题目
（2013•永州一模）已知函数f（x）=mlnx+
1
x
，（其中m为常数）
（1）试讨论f（x）在区间（0，+∞）上的单调性；
（2）令函数h（x）=f（x）+
1
m
lnx-x．当m∈[2，+∞）时，曲线y=h（x）上总存在相异两点P（x1，f（x1））、Q（x2，f（x2）），使得过P、Q点处的切线互相平行，求x1+x2的取值范围．
（2013•永州一模）提高大桥的车辆通行能力可改善整个城市的交通状况．一般情况下，大桥上的车流速度v（单位：千米/小时）是车流密度x（单位：辆/千米）的函数．当车流密度不超过50辆/千米时，车流速度为30千米/小时．研究表明：当50＜x≤200时，车流速度v与车流密度x满足v(x)=40-
k
250-x
．当桥上的车流密度达到200辆/千米时，造成堵塞，此时车流速度为0千米/小时．
（Ⅰ）当0＜x≤200时，求函数v（x）的表达式；
（Ⅱ）当车流密度x为多大时，车流量（单位时间内通过桥上观测点的车辆数，单位：辆/小时）f（x）=x•v（x）可以达到最大，并求出最大值．（精确到个位，参考数据
5
≈2.236）
（2013•永州一模）已知A，B是圆C（为圆心）上的两点，|
AB
|=2，则
AB
•
AC
=
2
2
．
（2013•永州一模）设集合A={x|-1＜x＜2}，B={x|x2≤1}，则A∩B=（　　）
（2013•永州一模）“x≠3”是“|x-3|＞0”的（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网