题目内容
下列“p或q”形式的复合命题为假命题的是( )
| A、p:2为质数q:1为质数 | ||||
B、p:(
| ||||
| C、p:奇数集为x|x=4n+1,n∈Zq:偶数集为{x|x=4n,n∈Z} | ||||
| D、p:CIA∪CIB=CI(A∩B)q:CIA∩CIB=CI(A∪B) |
分析:根据“p或q”形式的复合命题为假命题,当且仅当p、q都是假命题时,因此对选项中的每个命题逐个判定,即可得到答案,
A、2是质数,1既不是质数又不是合数,
B、(
)6=8为有理数,
C、奇数集{x|x=2n+1,n∈Z},偶数集为{x|x=2n,n∈Z},
D、CIA∪CIB=CI(A∩B),CIA∩CIB=CI(A∪B)都是要掌握的结论.
A、2是质数,1既不是质数又不是合数,
B、(
| 2 |
C、奇数集{x|x=2n+1,n∈Z},偶数集为{x|x=2n,n∈Z},
D、CIA∪CIB=CI(A∩B),CIA∩CIB=CI(A∪B)都是要掌握的结论.
解答:解:A、p:2为质数,正确;q:1为质数,错,因此“p或q”是真命题;
B、p:(
)3=2
为无理数,正确;q:(
)6=8为无理数,错,因此“p或q”是真命题;
C、p:奇数集为{x|x=4n+1,n∈Z},错;q:偶数集为{x|x=4n,n∈Z},错;因此“p或q”是假命题;
D、p:CIA∪CIB=CI(A∩B),正确;q:CIA∩CIB=CI(A∪B),正确;因此因此“p或q”是真命题;
故选C.
B、p:(
| 2 |
| 2 |
| 2 |
C、p:奇数集为{x|x=4n+1,n∈Z},错;q:偶数集为{x|x=4n,n∈Z},错;因此“p或q”是假命题;
D、p:CIA∪CIB=CI(A∩B),正确;q:CIA∩CIB=CI(A∪B),正确;因此因此“p或q”是真命题;
故选C.
点评:此题考查复合命题“p或q”的真假,都假才为假、“p且q”的真假,都真才为真、“非p”与p真假相反,属基础题.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
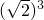 为无理数q:
为无理数q: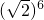 为无理数
为无理数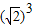 为无理数q:
为无理数q: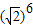 为无理数
为无理数