题目内容
已知△ABC是等腰直角三角形，∠C=90°，AB=2| 2 |
| AB |
| BC |
分析：根据三角形是一个等腰三角形，得到BC线段的长度，从而得到对应向量的模长，根据两个向量的位置关系，看出两个向量的夹角是三角形内角的补角，利用数量积公式得到结果．
解答：解：由题意知，
与
的夹角是135°，
∵|
|=2
，
∴|
|=2
×
=2，
∴
•
=-2
×2×
=-4，
故答案为：-4
| AB |
| BC |
∵|
| AB |
| 2 |
∴|
| BC |
| 2 |
| ||
| 2 |
∴
| AB |
| BC |
| 2 |
| ||
| 2 |
故答案为：-4
点评：本题是一个求两个向量数量积的问题，应用数量积的定义，在解题过程中注意应用条件中所给的模长和夹角的条件，这是一个典型的数量积的应用．是一个易错题．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
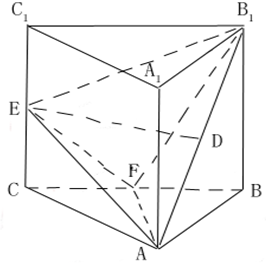如图，已知直三棱柱ABC-A1B1C1中，△ABC是等腰直角三角形，∠BAC=90°，且AB=AA1，D、E、F分别是B1A、CC1、BC的中点．现设A1A=2a
（2013•丽水一模）已知直三棱柱ABC-A1B1C1，底面△ABC是等腰三角形，∠BAC=120°，
