题目内容
如图所示，已知PA与⊙O相切，A为切点，PBC为割线，，弦CD∥AP，AD、BC相交于E点，F为CE上一点，且DE2=EF·EC.
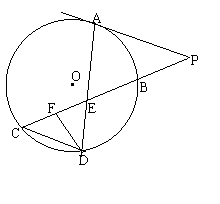（1）求证：ÐP=ÐEDF；
(2)求证：CE·EB=EF·EP．
证明：（1）∵DE2=EF·EC，
∴DE : CE=EF: ED．
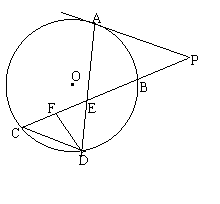∵ÐDEF是公共角，
∴ΔDEF∽ΔCED． ∴ÐEDF=ÐC．
∵CD∥AP， ∴ÐC=Ð P．
∴ÐP=ÐEDF．…………………………5分
（2）∵ÐP=ÐEDF， ÐDEF=ÐPEA，
∴ΔDEF∽ΔPEA． ∴DE : PE=EF : EA．
即EF·EP=DE·EA．
∵弦AD、BC相交于点E，
∴DE·EA=CE·EB．∴CE·EB=EF·EP．………………………… 10分
练习册系列答案
阅读快车系列答案
相关题目
22、如图所示，已知PA与⊙O相切，A为切点，PBC为割线，，弦CD∥AP，AD、BC相交于E点，F为CE上一点，且DE2=EF•EC．
（选修4-1：几何证明选讲）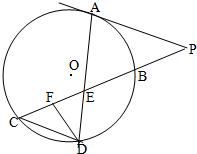
如图所示，已知PA与⊙O相切，A为切点，PBC为割线，，弦CD∥AP，AD、BC相交于E点，F为CE上一点，且DE2=EF•EC．
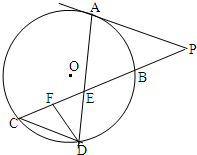如图所示，已知PA与⊙O相切，A为切点，PBC为割线，，弦CD∥AP，AD、BC相交于E点，F为CE上一点，且DE2=EF•EC．
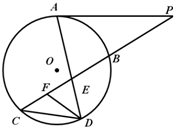（2013•甘肃三模）选修4-1：几何证明选讲