题目内容
已知函数f(x)=2cosx•sin(x+
)-
.
(1)求函数f(x)的最小正周期T;
(2)在给定的坐标系中,用“五点法”作出函数f(x)在一个周期上的函数.
| π |
| 3 |
| ||
| 2 |
(1)求函数f(x)的最小正周期T;
(2)在给定的坐标系中,用“五点法”作出函数f(x)在一个周期上的函数.

(1)f(x)=2cosx•sin(x+
)-
=2cosx(sinxcos
+cosxsin
)-
=2cosx(
sinx+
cosx)-
=sinxcosx+
•cos2x-
=
sin2x+
•
-
=
sin2x+
cos2x
=sin(2x+
).
∴T=
=
=π.
即函数f(x)的最小正周期为π.
(2)列表:
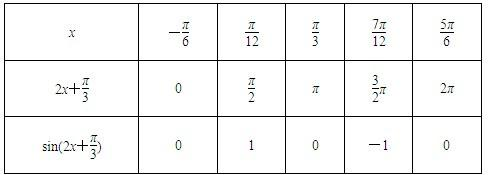
描点画图:
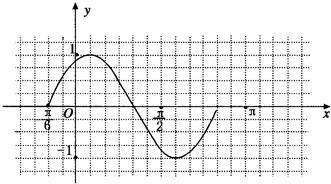
| π |
| 3 |
| ||
| 2 |
=2cosx(sinxcos
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
=2cosx(
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
=sinxcosx+
| 3 |
| ||
| 2 |
=
| 1 |
| 2 |
| 3 |
| 1+cos2x |
| 2 |
| ||
| 2 |
=
| 1 |
| 2 |
| ||
| 2 |
=sin(2x+
| π |
| 3 |
∴T=
| 2π |
| |w| |
| 2π |
| 2 |
即函数f(x)的最小正周期为π.
(2)列表:

描点画图:


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目