题目内容
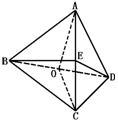
如图,四面体ABCD的棱BD长为2,其余各棱的长均是![]() ,求:二面角A—BD—C、A—BC—D、B—AC—D的大小.
,求:二面角A—BD—C、A—BC—D、B—AC—D的大小.
解析:
(1)取BD的中点O,连AO、OC.在ΔABD中,∵AB=AD=![]() ,BD=2,
,BD=2,
∴ΔABD是等腰直角三角形,AO⊥BD,同理OC⊥BD.
∴∠AOC是二面角A—BD—C的平面角
又AO=OC=1,AC=![]() ,∴∠AOC=90°.即二面角A—BD—C为直二面角.
,∴∠AOC=90°.即二面角A—BD—C为直二面角.
(2)∵二面角A—BD—C是直二面角,AO⊥BD,∴AO⊥平面BCD.
∴ΔABC在平面BCD内的射影是ΔBOC.
∵SΔOCB=![]() ,SΔABC=
,SΔABC=![]() ,∴cosθ=
,∴cosθ=![]() .即二面角A—BC—D的大小是arccos
.即二面角A—BC—D的大小是arccos![]() .
.
(3)取AC的中点E,连BE、DE.∵AB=BC,AD=DC,
∴BD⊥AC,DE⊥AC,∴∠BED就是二面角的平面角.
在ΔBDE中,BE=DE=![]() ,由余弦定理,得cosα=-
,由余弦定理,得cosα=-![]()
∴二面角B—AC—D的大小是π-arccos![]() .
.
评析 本例提供了求二面角大小的方法:先作出二面角的平面角,再利用其所在的三角形算出角的三角函数值,或利用面积的射影公式S′=S·cosθ求得.

练习册系列答案
相关题目
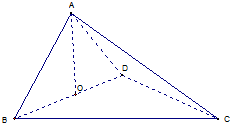 如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形,
如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形, 如图,四面体ABCD中,0是BD的中点,CA=CB=CD=BD=a,AB=AD=
如图,四面体ABCD中,0是BD的中点,CA=CB=CD=BD=a,AB=AD= 如图,四面体ABCD的各个面都是直角三角形,已知AB⊥BC,BC⊥CD,AB=a,BC=a,CD=c.
如图,四面体ABCD的各个面都是直角三角形,已知AB⊥BC,BC⊥CD,AB=a,BC=a,CD=c.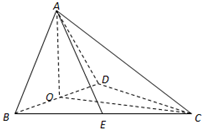 如图,四面体ABCD中,O、E分别是BD、BC的中点,AO⊥平面BCD,CA=CB=CD=BD=2.
如图,四面体ABCD中,O、E分别是BD、BC的中点,AO⊥平面BCD,CA=CB=CD=BD=2.