题目内容
口袋中有质地、大小完全相同的5个球,编号分别为1、2、3、4、5,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.(1)求两个编号的和为6的概率;
(2)求甲赢的事件发生的概率.
分析:(1)本题是一个古典概型,试验发生包含的甲、乙两人取出的数字共有5×5种等可能的结果,满足条件的事件可以通过列举法得到,根据古典概型的概率公式得到结果.
(2)要求甲赢的事件发生的概率,根据甲、乙摸到球的编号只能同奇同偶结合古典概型做出甲胜的概率得到结论.
(2)要求甲赢的事件发生的概率,根据甲、乙摸到球的编号只能同奇同偶结合古典概型做出甲胜的概率得到结论.
解答:解:(1)编号的和为6
甲、乙只能取(1,5),(2,4),(3,3),(4,2),(5,1),
∴P=
×5=
(2)甲、乙摸到球的编号只能同奇同偶
若甲摸到奇数,则P=
•
=
,
若甲摸到偶数,则P=
•
=
∴甲赢的概率为
.
甲、乙只能取(1,5),(2,4),(3,3),(4,2),(5,1),
∴P=
| 1 |
| 25 |
| 1 |
| 5 |
(2)甲、乙摸到球的编号只能同奇同偶
若甲摸到奇数,则P=
| 3 |
| 5 |
| 3 |
| 5 |
| 9 |
| 25 |
若甲摸到偶数,则P=
| 2 |
| 5 |
| 2 |
| 5 |
| 4 |
| 25 |
∴甲赢的概率为
| 13 |
| 25 |
点评:本题考查古典概型及其概率公式,考查利用列举法得到试验包含的所有事件,考查利用概率知识解决实际问题,本题好似一个典型的概率题目.

练习册系列答案
相关题目
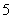 个球,编号分别为
个球,编号分别为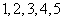 ,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.
,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.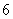 的事件发生的概率;
的事件发生的概率;