题目内容
已知点P是边长a的正三角形ABC边上的任意一点，则| PA2 |
| PB2 |
| PC2 |
分析：通过建立坐标系，将向量模的平方的最大值转化为函数的最值．
解答：解：不妨设点P在边BC上，以BC所在直线为x轴，以BC边上的高为y轴，建立直角坐标系，
则B（-
，0)，C(
，0)，A（0，
a）
故
+
+
=x2+
a2+(x+
)2+(x-
)2
=3x2+
a2≥
a2
故
+
+
的最小值为
a2
则B（-
| a |
| 2 |
| a |
| 2 |
| ||
| 2 |
故
| PA2 |
| PB2 |
| PC2 |
| 3 |
| 4 |
| a |
| 2 |
| a |
| 2 |
=3x2+
| 5 |
| 4 |
| 5 |
| 4 |
故
| PA2 |
| PB2 |
| PC2 |
| 5 |
| 4 |
点评：本题考查数学中的等价转化的能力及求函数的最值．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
已知P是边长为2的正△ABC的边BC上的动点，则
•(
+
)（ ）
| AP |
| AB |
| AC |
| A、最大值为8 | B、是定值6 |
| C、最小值为2 | D、是定值2 |
边BC上的动点，则
（ ）
边BC上的动点，则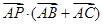
（ ）