Question

设M={1,2,3,…,20},任取x,y∈M,x≠y,求:

(1)x+y恰好是3的倍数的概率;

(2)xy恰好是3的倍数的概率.

Answer 1

解析:本题主要考查的是排列组合的知识,互斥事件及对立事件的定义及其概率公式,对分类讨论思想及综合分析,解决问题的能力要求较高.?

(1)因x+y恰是3的倍数,故需对M中的数分类为3k,3k+1,3k+2(k∈Z),只有当两数均取自于第一类或第二\,三类各取一个时,其和才是3的倍数.?

(2)xy是3的倍数,只要其中有一个是3的倍数就够了.?

设M₀={3,6,9,12,15,18},M₁={1,4,7,10,13,16,19},M₂={2,5,8,11,14,17,20},则card(M₀)=6,card(M₁)=7,card(M₂)=7.?

(1)方法一:采用无序讨论(不考虑x和y的先后顺序),?

设事件A为“从M中任取2个数,其和是3的倍数”,由于任一个和“x+y”的获得是等可能的,则基本事件的总数为n= .?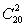

“x+y恰为3的倍数”可由两个事件构成,一是x\,y∈M₀(记为事件B),二是x∈M₁,y∈M₂或x∈M₂,y∈M₁(记为事件C),则构成事件A的基本事件数为m=C²₆+C¹₇C¹₇ ,则由等可能事件的概率公式得事件A发生的概率为?

P(A)=.?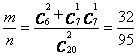

方法二:采用有序讨论(要考虑x和y的先后顺序),?

同样事件A为“从M中任取2个数,其和是3的倍数”,则基本事件的总数为n′=A²₂₀=2n,构成事件A的基本事件数为m′=A²₆+C¹₇C¹₇A²₂=2m,则事件A发生的概率为?

P(A)=.?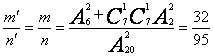

(2)方法一:直接法(分类讨论).?

设事件D表示“xy恰好是3的倍数”,若不考虑x和y的先后顺序,基本事件的总数为n=C²₂₀,事件D也可由两个事件构成,一是x、y∈M₀,二是x∈M₀,y∈M₁∪M₂或y∈M₀,x∈M₁∪M₂,则构成事件D的基本事件数为m=C²₆+C¹₆C¹₇+C¹₆C¹₇ ,由等可能事件的概率公式得事件D发生的概率为?

P(D)=.?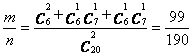

方法二:间接法(先求其对立事件的概率).?

设事件“xy恰好是3的倍数”的对立事件为,“xy不是3的倍数”等价于“x和y都不是3的倍数”.基本事件的总数仍为n=C²₂₀?,构成事件D的基本事件数为m=C²₁₄ ,则事件D发生的概率为?

P(D)=1-P()=1-.?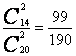

若考虑x和y的先后顺序结果也是一样.?

点评:(1)的问题用了无序和有序两种方法进行考虑,结果一样,(2)的问题利用了对立事件的概率,简化了计算,(1)和(2)中都采用了对复杂问题进行拆分的手段,不仅仅便于计算基本事件数,关键性的作用是避免了重复和遗漏.