题目内容
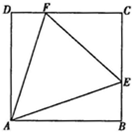
如图所示，点E在△ABC的边BC上，且CE=3EB，设| AB |
| a |
| AC |
| b |
| AE |
| 3 |
| 4 |
| a |
| 1 |
| 4 |
| b |
| 3 |
| 4 |
| a |
| 1 |
| 4 |
| b |
| a |
| b |
分析：由CE=3EB，可得
=
．又由
=
-
，可得
=
+
=
+
．
| BE |
| 1 |
| 4 |
| BC |
| BC |
| AC |
| AB |
| AE |
| AB |
| BE |
| AB |
| 1 |
| 4 |
| BC |
解答：解：∵CE=3EB，∴
=
．
又∵
=
-
，
∴
=
+
=
+
=
+
(
-
)=
+
．
故答案为
+
．
| BE |
| 1 |
| 4 |
| BC |
又∵
| BC |
| AC |
| AB |
∴
| AE |
| AB |
| BE |
| AB |
| 1 |
| 4 |
| BC |
=
| a |
| 1 |
| 4 |
| b |
| a |
| 3 |
| 4 |
| a |
| 1 |
| 4 |
| b |
故答案为
| 3 |
| 4 |
| a |
| 1 |
| 4 |
| b |
点评：熟练掌握向量共线定理和三角形法则即可得出．
练习册系列答案
相关题目
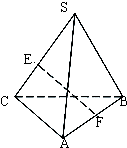如图所示，点S在平面ABC外，SB⊥AC，SB=AC=2，E、F分别是SC和AB的中点，则EF的长是（ ）| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
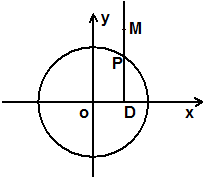如图所示，点P在圆O：x2+y2=4上，PD⊥x轴，点M在射线DP上，且满足
