题目内容
已知椭圆![]() ,离心率为
,离心率为![]() 的椭圆经过点
的椭圆经过点![]() 。
。
(1)求该椭圆的标准方程;
(2)过椭圆的一个焦点且互相垂直的直线![]() 分别与椭圆交于A,B和C,D,是否存在常数
分别与椭圆交于A,B和C,D,是否存在常数![]() ,使得
,使得![]() ?若存在,求出实数
?若存在,求出实数![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
解:(1)设椭圆方程为![]() ,则
,则![]() ,即
,即![]() ,
,
由此得![]() ,故椭圆方程是
,故椭圆方程是![]() ,
,
将点![]() 的坐标代入,得
的坐标代入,得![]() ,解得
,解得![]() ,
,
故椭圆方程是![]() 。
。
(2)问题等价于![]() ,即
,即![]() 是否是定值问题。
是否是定值问题。
椭圆的焦点坐标是![]() ,不妨取焦点(2,0),
,不妨取焦点(2,0),
(i)当直线AB的斜率存在且不等于零时,
设直线AB的斜率为k,则直线AB的方程是![]() ,
,
代入椭圆方程并整理得![]() 。
。
设![]() ,则
,则![]() 。
。
根据弦长公式,
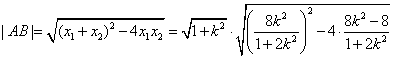

以![]() 代换k,得
代换k,得
所以![]()
即![]()
(ii)当直线AB的斜率不存在或等于零时,![]() 一个是长轴长度,一个是通径长度,此时
一个是长轴长度,一个是通径长度,此时![]() ,即
,即![]() 。
。
综上所述,故存在实数![]() ,使得
,使得![]() 。
。

练习册系列答案
相关题目

 是离心率为
是离心率为 的椭圆
的椭圆 :
: 上的一点,斜率为
上的一点,斜率为 的直线
的直线 交椭圆
交椭圆 、
、 两点,且
两点,且 、
、 的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由?
的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由?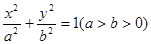 ,离心率为
,离心率为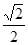 的椭圆经过点
的椭圆经过点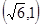 .
. 分别与椭圆交于
分别与椭圆交于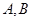 和
和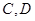 ,是否存在常数
,是否存在常数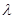 ,使得
,使得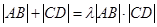 ?若存在,求出实数
?若存在,求出实数