题目内容
已知函数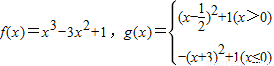 ,则方程g[f(x)]-a=0(a为正实数)的实数根最多有( )个.
,则方程g[f(x)]-a=0(a为正实数)的实数根最多有( )个.A.6个
B.4个
C.7个
D.8个
【答案】分析:利用导数求的f(x)的极大值为f(0)=1,极小值为f(2)=-3,且函数的值域为R.分a=1、0<a<1、a>1三种
情况,研究方程跟的个数,从而得出结论.
解答:解:∵函数 ,
,
令f′(x)=0 可得 x=0,x=2,在(-∞,0)上,f′(x)>0,f(x)是增函数;
在(0,2)上,f′(x)<0,f(x)是减函数;在(2,+∞)上,f′(x)>0,f(x)是增函数.
故f(x)的极大值为f(0)=1,极小值为f(2)=-3,且函数的值域为R.
由函数g(x)的图象可得,当x=-3或x= 时,g(x)=1.
时,g(x)=1.
①当a=1时,若方程g[f(x)]-a=0,则:
f(x)=-3,此时方程有2个根,或f(x)= ,此时方程有3个根,
,此时方程有3个根,
故方程g[f(x)]-a=0可能共有5个根.
②当0<a<1时,方程g[f(x)]-a=0,则:
f(x)∈(-4,-3),此时方程有1个根,或f(x)∈(-3,-2),此时方程有3个根
故方程g[f(x)]-a=0可能共有4个根.
③当a>1时,方程g[f(x)]-a=0,则:f(x)∈(0, ),或f(x)∈(
),或f(x)∈( ,+∞),
,+∞),
方程可能有4个、5个或6个根.
故方程g[f(x)]-a=0(a为正实数)的实数根最多有6个,
故选 A.
点评:本题考查的知识点是根的存在性及根的个数判断,其中分析内外函数的图象是解答本题的关键,属于中档题.
情况,研究方程跟的个数,从而得出结论.
解答:解:∵函数
 ,
,令f′(x)=0 可得 x=0,x=2,在(-∞,0)上,f′(x)>0,f(x)是增函数;
在(0,2)上,f′(x)<0,f(x)是减函数;在(2,+∞)上,f′(x)>0,f(x)是增函数.
故f(x)的极大值为f(0)=1,极小值为f(2)=-3,且函数的值域为R.
由函数g(x)的图象可得,当x=-3或x=
 时,g(x)=1.
时,g(x)=1.①当a=1时,若方程g[f(x)]-a=0,则:
f(x)=-3,此时方程有2个根,或f(x)=
 ,此时方程有3个根,
,此时方程有3个根,故方程g[f(x)]-a=0可能共有5个根.
②当0<a<1时,方程g[f(x)]-a=0,则:
f(x)∈(-4,-3),此时方程有1个根,或f(x)∈(-3,-2),此时方程有3个根
故方程g[f(x)]-a=0可能共有4个根.
③当a>1时,方程g[f(x)]-a=0,则:f(x)∈(0,
 ),或f(x)∈(
),或f(x)∈( ,+∞),
,+∞),方程可能有4个、5个或6个根.
故方程g[f(x)]-a=0(a为正实数)的实数根最多有6个,
故选 A.
点评:本题考查的知识点是根的存在性及根的个数判断,其中分析内外函数的图象是解答本题的关键,属于中档题.

练习册系列答案
相关题目
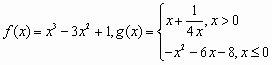 ,则方程g[f(x)]-a=0(a为正实数)的根的个数不可能为
,则方程g[f(x)]-a=0(a为正实数)的根的个数不可能为 ,则方程g[f(x)]-a=0(a为正实数)的实数根最多有______个.
,则方程g[f(x)]-a=0(a为正实数)的实数根最多有______个.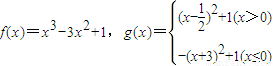 ,则方程g[f(x)]-a=0(a为正实数)的实数根最多有( )个.
,则方程g[f(x)]-a=0(a为正实数)的实数根最多有( )个.