题目内容
对于函数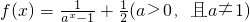
（1）判断函数f（x）的奇偶性；
（2）探究函数f（x）在（0，+∞）上的单调性，并用定义加以证明；
（3）当2＜a＜4时，求函数f（x）在[-3，-1]上的最大值和最小值．
解：（1）由ax-1≠0，得x≠0，∴定义域为（-∞，0）∪（0，+∞），关于原点对称．
∵
，
∴f（x）为奇函数．
（2）任取x1，x2∈（0，+∞），且x1＜x2，则f（x1）-f（x2）=
-
=
，
①当0＜a＜1时，
=1，∴
＜0，
，
，∴f（x1）-f（x2）＜0，即f（x1）＜f（x2），∴f（x）单调递增；
②当a＞1时，
，∴
，
，
，∴f（x1）-f（x2）＞0，即f（x1）＞f（x2），∴f（x）单调递减．
综上，当0＜a＜1时，f（x）在（0，+∞）为增函数；当a＞1时，f（x）在（0，+∞）为减函数．
（3）由（2）知：当2＜a＜4时，函数f（x）在[1，3]上是减函数，由（1）知：f（x）为奇函数，所以f（x）在[-3，-1]上也为减函数，则
．
分析：（1）先求函数f（x）的定义域看是否关于原点对称，若对称，再依据f（-x）与f（x）的关系作出判断．
（2）先设0＜x1＜x2，再比较f（x1）与f（x2）的大小关系，依据定义作出判断，其间要对a进行讨论．
（3）本题可利用（1），（2）问的结论求出．
点评：本题主要考查函数的奇偶性、单调性，利用定义是解决该类问题的常用办法．
∵
，∴f（x）为奇函数．
（2）任取x1，x2∈（0，+∞），且x1＜x2，则f（x1）-f（x2）=
-=，①当0＜a＜1时，
=1，∴＜0，，，∴f（x1）-f（x2）＜0，即f（x1）＜f（x2），∴f（x）单调递增；②当a＞1时，
，∴，，，∴f（x1）-f（x2）＞0，即f（x1）＞f（x2），∴f（x）单调递减．综上，当0＜a＜1时，f（x）在（0，+∞）为增函数；当a＞1时，f（x）在（0，+∞）为减函数．
（3）由（2）知：当2＜a＜4时，函数f（x）在[1，3]上是减函数，由（1）知：f（x）为奇函数，所以f（x）在[-3，-1]上也为减函数，则
．分析：（1）先求函数f（x）的定义域看是否关于原点对称，若对称，再依据f（-x）与f（x）的关系作出判断．
（2）先设0＜x1＜x2，再比较f（x1）与f（x2）的大小关系，依据定义作出判断，其间要对a进行讨论．
（3）本题可利用（1），（2）问的结论求出．
点评：本题主要考查函数的奇偶性、单调性，利用定义是解决该类问题的常用办法．
练习册系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
某研究性学习小组研究函数f（x）=ax3+bx（a≠0，a，b为常数）的 性质：
（Ⅰ）甲同学得到如下表所示的部分自变量x及其对应函数值y的近似值（精确到0.01）：
请你根据上述表格中的数据回答下列问题：
（i）函数f（x）在区间（0.4，0.44）内是否存在零点，写出你的判断并加以证明；
（ii）证明：函数f（x）在区间（-∞，-0.3）上单调递减；
（Ⅱ）乙同学发现对于函数f（x）图象上的两点A（-1，4），B（t，f（t））（-1＜t＜2），存在m∈（-1，t），使f'（m）的值恰为直线AB的斜率，请你判断乙同学的结论是否正确？若正确，请给出证明并确定m的个数，若不正确，请说明理由．
（Ⅰ）甲同学得到如下表所示的部分自变量x及其对应函数值y的近似值（精确到0.01）：
| x | -1 | -0.72 | -0.44 | -0.16 | 0.12 | 0.4 |
| y的近似值 | 4.00 | 1.15 | 0.02 | -0.14 | 0.11 | 0.08 |
（i）函数f（x）在区间（0.4，0.44）内是否存在零点，写出你的判断并加以证明；
（ii）证明：函数f（x）在区间（-∞，-0.3）上单调递减；
（Ⅱ）乙同学发现对于函数f（x）图象上的两点A（-1，4），B（t，f（t））（-1＜t＜2），存在m∈（-1，t），使f'（m）的值恰为直线AB的斜率，请你判断乙同学的结论是否正确？若正确，请给出证明并确定m的个数，若不正确，请说明理由．
某研究性学习小组研究函数f（x）=ax3+bx（a≠0，a，b为常数）的 性质：
（Ⅰ）甲同学得到如下表所示的部分自变量x及其对应函数值y的近似值（精确到0.01）：
| x | -1 | -0.72 | -0.44 | -0.16 | 0.12 | 0.4 |
| y的近似值 | 4.00 | 1.15 | 0.02 | -0.14 | 0.11 | 0.08 |
（i）函数f（x）在区间（0.4，0.44）内是否存在零点，写出你的判断并加以证明；
（ii）证明：函数f（x）在区间（-∞，-0.3）上单调递减；
（Ⅱ）乙同学发现对于函数f（x）图象上的两点A（-1，4），B（t，f（t））（-1＜t＜2），存在m∈（-1，t），使f'（m）的值恰为直线AB的斜率，请你判断乙同学的结论是否正确？若正确，请给出证明并确定m的个数，若不正确，请说明理由．
某研究性学习小组研究函数f（x）=ax3+bx（a≠0，a，b为常数）的 性质：
（Ⅰ）甲同学得到如下表所示的部分自变量x及其对应函数值y的近似值（精确到0.01）：
请你根据上述表格中的数据回答下列问题：
（i）函数f（x）在区间（0.4，0.44）内是否存在零点，写出你的判断并加以证明；
（ii）证明：函数f（x）在区间（-∞，-0.3）上单调递减；
（Ⅱ）乙同学发现对于函数f（x）图象上的两点A（-1，4），B（t，f（t））（-1＜t＜2），存在m∈（-1，t），使f'（m）的值恰为直线AB的斜率，请你判断乙同学的结论是否正确？若正确，请给出证明并确定m的个数，若不正确，请说明理由．
（Ⅰ）甲同学得到如下表所示的部分自变量x及其对应函数值y的近似值（精确到0.01）：
| x | -1 | -0.72 | -0.44 | -0.16 | 0.12 | 0.4 |
| y的近似值 | 4.00 | 1.15 | 0.02 | -0.14 | 0.11 | 0.08 |
（i）函数f（x）在区间（0.4，0.44）内是否存在零点，写出你的判断并加以证明；
（ii）证明：函数f（x）在区间（-∞，-0.3）上单调递减；
（Ⅱ）乙同学发现对于函数f（x）图象上的两点A（-1，4），B（t，f（t））（-1＜t＜2），存在m∈（-1，t），使f'（m）的值恰为直线AB的斜率，请你判断乙同学的结论是否正确？若正确，请给出证明并确定m的个数，若不正确，请说明理由．