题目内容
3.已知D、E分别为△ABC边AB、AC的中点,F是线段DE上一点,BF交AC于点C,CF交AB于点H,求$\frac{AG}{GC}+\frac{AH}{HB}$的值.分析 以B为坐标原点,以BC为x轴正方向建立坐标系,设C(2a,0),A(2b,2c),则D(b,c),E(a+b,c),设F点坐标为(t,c),求出G,H点坐标,进而可得$\frac{AG}{GC}+\frac{AH}{HB}$的值.
解答 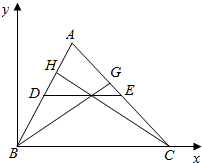 解:如图所示,以B为坐标原点,以BC为x轴正方向建立坐标系,
解:如图所示,以B为坐标原点,以BC为x轴正方向建立坐标系,
设C(2a,0),A(2b,2c),则D(b,c),E(a+b,c),
设F点坐标为(t,c),
则直线BG的方程为:y=$\frac{c}{t}$x,
直线AC的方程为:y=$\frac{c}{b-a}$(x-2a),
联立直线AC与BD的方程可得:$\frac{c}{t}$x=$\frac{c}{b-a}$(x-2a),
解得:x=$\frac{2t}{a+t-b}$,
故$\frac{AG}{GC}$=$\frac{\frac{2at}{a+t-b}-2b}{2a-\frac{2at}{a+t-b}}$=$\frac{at-ab-bt+{b}^{2}}{{a}^{2}-ab}$,
同理可得:$\frac{AH}{HB}$=$\frac{a+b-t}{a}$,
∴$\frac{AG}{GC}+\frac{AH}{HB}$=$\frac{at-ab-bt+{b}^{2}}{{a}^{2}-ab}$+$\frac{a+b-t}{a}$=1
点评 本题考查的知识点是直线的交点坐标,建立坐标系,求出点的坐标,是解答的关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
11.下列有关命题的说法正确的是( )
| A. | 命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” | |
| B. | 命题“?x∈R,使得x2+x+1<0”的否定是:“?x∈R 均有x2+x+1<0” | |
| C. | 在△ABC中,“A>B”是“sinA>sinB”的充要条件 | |
| D. | “x≠2或y≠1”是“x+y≠3”既不充分也不必要条件 |
12.为了解某校学生喜爱打篮球是否与性别有关,采用随机抽样方法抽取了50名学生进行问卷调查,得到如下的列联表:
已知在这50名学生中随机抽取1人,抽到喜爱打篮球的学生的概率为$\frac{3}{5}$.
(Ⅰ)请将上面的列联表补充完整;
(Ⅱ)是否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由;
(Ⅲ)记不喜爱打篮球的5名男生分别为A、B、C、D、E,这5名男生喜爱打乒乓球,
如果从他们当中任选2人作为一对组合参加乒乓球男子双打比赛,求A、B中恰好有1人被选中的概率.
下面的临界值表供参考:
(参考公式:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 5 | ||
| 女生 | 10 | ||
| 合计 | 50 |
(Ⅰ)请将上面的列联表补充完整;
(Ⅱ)是否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由;
(Ⅲ)记不喜爱打篮球的5名男生分别为A、B、C、D、E,这5名男生喜爱打乒乓球,
如果从他们当中任选2人作为一对组合参加乒乓球男子双打比赛,求A、B中恰好有1人被选中的概率.
下面的临界值表供参考:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |