题目内容
已知函数f(x)=logax(a>0且a≠1),若数列2,f(a1),f(a2),…,f(an),2n+4(n∈N*)成等差数列.(1)求数列{an}的通项an;
(2)若0<a<1,求数列{an}的前n项和Sn;
(3)若a=2,令bn=an·f(an),对任意n∈N*,都有bn>f-1(t),求实数t的取值范围.
解:(1)2n+4=2+(n+2-1)d,∴d=2.
∴f(an)=2+(n+1-1)·2=2n+2.
∴an=a2n+2.
(2)Sn=![]() .
.
(3)bn=an·f(an)=(2n+2)a2n+2=(2n+2)·22n+2=(n+1)·22n+3,![]() ·4>1,∴bn+1>bn.∴{bn}为递增数列.∴bn中最小项为b1=2·25=26,f-1(t)=2t.
·4>1,∴bn+1>bn.∴{bn}为递增数列.∴bn中最小项为b1=2·25=26,f-1(t)=2t.
∴26>2t.∴t<6.

练习册系列答案
相关题目







 x
x -ax+(a-1)
-ax+(a-1) ,
, 。讨论函数
。讨论函数 的单调性;
的单调性; 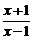 ,求函数φ (x)的单调区间;
,求函数φ (x)的单调区间;