Question

某同学上楼梯的习惯每步走1阶或2阶，现有一个11阶的楼梯 ，该同学从第1阶到第11阶用7步走完。

(1)求该同学恰好有连着三步都走2阶的概率；

(2)记该同学连走2阶的最多步数为ζ，求随机事件ζ的分布列及其期望。

Answer 1

(1)该同学恰好有连着三步都走2阶的概率为

        (2) 随机事件ζ的分布列是

ξ	1	2	3	4
P

ξ的期望是

解析:

设走2阶的步数为x，走1阶的步数为y，则有

 (1) 

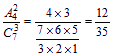
(2)P(ζ=1)= 

  P(ζ=3)=

随机事件ζ的分布列是

ξ	1	2	3	4
P

ξ的期望是Eξ=×1+×2+×3+×4=