题目内容
8.已知函数$f(x)=\sqrt{(x+1)(x-2)}$的定义域集合是A,函数$g(x)=\frac{1}{{\sqrt{{x^2}-(2a+1)x+{a^2}+a}}}$的定义域集合是B.(1)求集合A、B;
(2)若A∩B=A,求实数a的取值范围.
分析 (1)分别求出f(x),g(x)的定义域,得到集合A,B.
(2)由题意A是B的子集,可解出实数a的取值范围.
解答 解:(1)由(x+1)(x-2)≥0,解得x≤-1或x≥2,
∴A={x|x≤-1或x≥2};
由x2-(2a+1)x+a2+a>0,得到(x-a)(x-a-1)>0,
解得x<a,或x>a+1,
∴B={x|x<a,或x>a+1};
(2)由A∩B=A得A⊆B,因此$\left\{\begin{array}{l}{a>-1}\\{a+1<2}\end{array}$,
解得-1<a<1,
所以,所以实数a的取值范围是(-1,1).
点评 本题考查函数的定义域及其求法,并集及运算,是基础题.

练习册系列答案
相关题目
18.已知$\overrightarrow{a}$=(-3,2),$\overrightarrow{b}$=(-1,0),向量λ$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-2$\overrightarrow{b}$垂直,则实数λ的值为( )
| A. | $\frac{1}{7}$ | B. | -$\frac{1}{7}$ | C. | $\frac{1}{6}$ | D. | -$\frac{1}{6}$ |
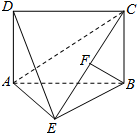 如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.
如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.