题目内容
请先阅读:在等式![]() ,
,
由求导法则,得![]() ,化简得等式:
,化简得等式:![]() .
.
(1)利用上题的想法(或其他方法),结合等式(1+x)n=![]() (
(![]() ,正整数
,正整数![]() ),证明:
),证明:![]() .
.
(2)对于正整数![]() ,求证:
,求证:
(i)![]() =0;
=0;
(ii)![]() =0;
=0;
(iii)![]() .
.
本题主要考查组合数、二项式定理、导数、积分等基础知识,考查推理论证能力与分析问题、解决问题的能力.
证明:(1)在等式![]() 两边对
两边对![]() 求导得
求导得
![]()
移项得 ![]() (*)
(*)
(2)(i)在(*)式中,令![]() ,整理得
,整理得 ![]()
所以 ![]()
(ii)由(1)知![]()
两边对![]() 求导,得
求导,得![]()
在上式中,令![]()
![]()
即 ![]() ,
,
亦即 ![]() (1)
(1)
又由(i)知 ![]() (2)
(2)
由(1)+(2)得![]()
(iii)将等式![]() 两边在
两边在![]() 上对
上对![]() 积分
积分![]()
由微积分基本定理,得![]()
所以 ![]() 。
。

练习册系列答案
相关题目

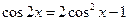 (
(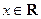 )的两边求导,得:
)的两边求导,得: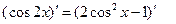 ,
, ,化简得等式:
,化简得等式: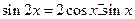 。
。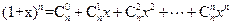 (
(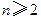 ),证明:
),证明: 。
。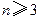 ,求证:
,求证: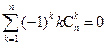 ; (ii)
; (ii)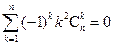 ; (iii)
; (iii)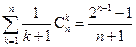 。
。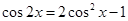 (
(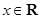 )的两边求导,得:
)的两边求导,得: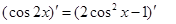 ,
,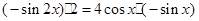 ,化简得等式:
,化简得等式: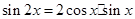 。
。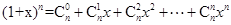 (
(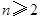 ),证明:
),证明: 。
。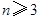 ,求证:
,求证: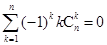 ; (ii)
; (ii)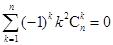 ; (iii)
; (iii)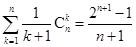 。
。