题目内容
14.已知直线l:y=2x+1,求:(1)直线l关于点M(3,2)对称的直线的方程;
(2)点M(3,2)关于l对称的点的坐标.
分析 (1)根据题意,点M不在直线l上,所求的直线l′与直线l平行,且点M到这两条直线的距离相等,设出直线l′的方程,利用距离公式求出它的方程;
(2)设出点M关于l对称的点N的坐标,利用对称轴的性质,列出方程组,求出对称点的坐标.
解答 解:(1)∵点M(3,2)不在直线l上,
∴所求的直线l′与直线l平行,且点M到这两条直线的距离相等;
设直线l′的方程为y=2x+b,
即2x-y+b=0,
∴$\frac{|2×3-2+b|}{\sqrt{{2}^{2}{+(-1)}^{2}}}$=$\frac{|2×3-2+1|}{\sqrt{{2}^{2}{+(-1)}^{2}}}$,
解得b=-9或b=1(不合题意,舍去),
∴所求的直线方程为2x-y-9=0;
(2)设点M(3,2)关于l对称的点为N(a,b),
则kMN=$\frac{b-2}{a-3}$=-$\frac{1}{2}$,
即a+2b=7①;
又MN的中点坐标为($\frac{a+3}{2}$,$\frac{b+2}{2}$),
且在直线l上,
∴$\frac{b+2}{2}$=2×$\frac{a+3}{2}$+1,
即2a-b=-2②;
由①、②组成方程组,解得$\left\{\begin{array}{l}{a=-1}\\{b=4}\end{array}\right.$,
∴所求的对称点为N(-1,4).
点评 本题考查了直线方程的应用问题,也考查了点关于直线的对称以及直线关于点的对称问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.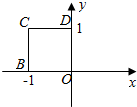 已知函数f(x)=$|\begin{array}{l}{x}\end{array}|,x∈[a,b]$值域是[0,1],那么点p(a,b) 在平面角坐标系中的位置位于图中的( )
已知函数f(x)=$|\begin{array}{l}{x}\end{array}|,x∈[a,b]$值域是[0,1],那么点p(a,b) 在平面角坐标系中的位置位于图中的( )
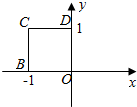 已知函数f(x)=$|\begin{array}{l}{x}\end{array}|,x∈[a,b]$值域是[0,1],那么点p(a,b) 在平面角坐标系中的位置位于图中的( )
已知函数f(x)=$|\begin{array}{l}{x}\end{array}|,x∈[a,b]$值域是[0,1],那么点p(a,b) 在平面角坐标系中的位置位于图中的( )| A. | 线段OB和OD | B. | 线段BC和CD | C. | 线段BC和BO | D. | 线段OB和CD |
4.二次函数f(x)=-x2+2x+1在闭区间[-1,0]上( )
| A. | 有最大值和最小值 | B. | 有最大值无最小值 | ||
| C. | 有最小值无最大值 | D. | 无最大值无最小值 |
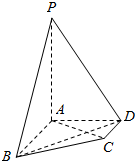 在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=2,AD=$\sqrt{2}$,CD=1,PA⊥平面ABCD,PA=2.
在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=2,AD=$\sqrt{2}$,CD=1,PA⊥平面ABCD,PA=2.