题目内容
已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=1-2-x,则不等式f(x)<- 的解集是
的解集是
- A.(-∞,-1)
- B.(-∞,-1]
- C.(1,+∞)
- D.[1,+∞)
A
分析:解不等式:“f(x)<- ”其中f(x)是指定义在R上的函数,而题目中只给出了x>0的表达式,故先求出当x<0时,f(x)的解析式,后再可解此不等式.
”其中f(x)是指定义在R上的函数,而题目中只给出了x>0的表达式,故先求出当x<0时,f(x)的解析式,后再可解此不等式.
解答:当x>0时,
1-2-x=1-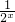 >0与题意不符,
>0与题意不符,
当x<0时,-x>0,∴f(-x)=1-2x,
又∵f(x)为R上的奇函数,
∴f(-x)=-f(x),
∴-f(x)=1-2x,∴f(x)=2x-1,
∴f(x)=2x-1<- ,∴2x<
,∴2x< ,
,
∴x<-1,∴不等式f(x)<- 的解集是(-∞,-1).
的解集是(-∞,-1).
故答案为A.
点评:本题的实质是已知奇函数的一半,求另一半的题型,必须充分注意利用奇函数的定义f(-x)=-f(x).
分析:解不等式:“f(x)<-
 ”其中f(x)是指定义在R上的函数,而题目中只给出了x>0的表达式,故先求出当x<0时,f(x)的解析式,后再可解此不等式.
”其中f(x)是指定义在R上的函数,而题目中只给出了x>0的表达式,故先求出当x<0时,f(x)的解析式,后再可解此不等式.解答:当x>0时,
1-2-x=1-
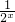 >0与题意不符,
>0与题意不符,当x<0时,-x>0,∴f(-x)=1-2x,
又∵f(x)为R上的奇函数,
∴f(-x)=-f(x),
∴-f(x)=1-2x,∴f(x)=2x-1,
∴f(x)=2x-1<-
 ,∴2x<
,∴2x< ,
,∴x<-1,∴不等式f(x)<-
 的解集是(-∞,-1).
的解集是(-∞,-1).故答案为A.
点评:本题的实质是已知奇函数的一半,求另一半的题型,必须充分注意利用奇函数的定义f(-x)=-f(x).

练习册系列答案
相关题目
 已知函数f(x)=x+
已知函数f(x)=x+