题目内容
已知函数f(x)=sin(x+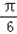 )+sin(x﹣
)+sin(x﹣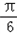 )+cosx+a(a∈R,a为常数).
)+cosx+a(a∈R,a为常数).
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)若函数f(x)在[﹣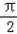 ,
,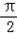 ]上的最大值与最小值之和为
]上的最大值与最小值之和为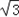 ,求实数a的值.
,求实数a的值.
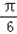 )+sin(x﹣
)+sin(x﹣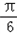 )+cosx+a(a∈R,a为常数).
)+cosx+a(a∈R,a为常数).(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)若函数f(x)在[﹣
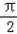 ,
,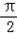 ]上的最大值与最小值之和为
]上的最大值与最小值之和为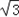 ,求实数a的值.
,求实数a的值.解:(Ⅰ)∵f(x)=sin(x+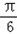 )+sin(x﹣
)+sin(x﹣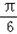 )+cosx+a
)+cosx+a
=sinxcos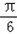 +cosxsin
+cosxsin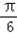 +sinxcos
+sinxcos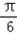 ﹣cosxsin
﹣cosxsin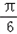 +cosx+a
+cosx+a
=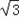 sinx+cosx+a
sinx+cosx+a
=2(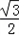 sinx+
sinx+ cosx)+a
cosx)+a
=2sin(x+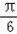 )+a,
)+a,
∴函数f(x)的最小正周期T=2π;
(Ⅱ)∵x∈[﹣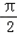 ,
,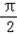 ],
],
∴﹣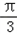 ≤x+
≤x+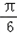 ≤
≤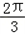 ,
,
∴当x+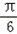 =﹣
=﹣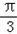 ,即x=﹣
,即x=﹣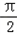 时,f(x)的最小值=f(﹣
时,f(x)的最小值=f(﹣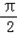 )=﹣
)=﹣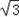 +a,
+a,
当x+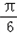 =
=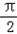 ,即x=
,即x=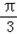 时,f(x)的最大值=f(
时,f(x)的最大值=f(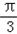 )=2+a,
)=2+a,
由题意,有(﹣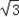 +a)+(2+a)=
+a)+(2+a)=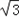 ,
,
∴a=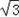 ﹣1.
﹣1.
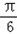 )+sin(x﹣
)+sin(x﹣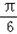 )+cosx+a
)+cosx+a=sinxcos
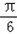 +cosxsin
+cosxsin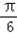 +sinxcos
+sinxcos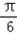 ﹣cosxsin
﹣cosxsin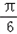 +cosx+a
+cosx+a=
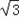 sinx+cosx+a
sinx+cosx+a=2(
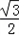 sinx+
sinx+ cosx)+a
cosx)+a=2sin(x+
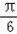 )+a,
)+a,∴函数f(x)的最小正周期T=2π;
(Ⅱ)∵x∈[﹣
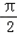 ,
,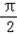 ],
],∴﹣
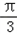 ≤x+
≤x+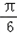 ≤
≤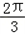 ,
,∴当x+
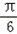 =﹣
=﹣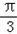 ,即x=﹣
,即x=﹣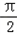 时,f(x)的最小值=f(﹣
时,f(x)的最小值=f(﹣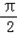 )=﹣
)=﹣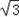 +a,
+a,当x+
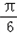 =
=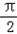 ,即x=
,即x=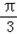 时,f(x)的最大值=f(
时,f(x)的最大值=f(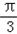 )=2+a,
)=2+a,由题意,有(﹣
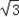 +a)+(2+a)=
+a)+(2+a)=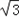 ,
,∴a=
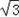 ﹣1.
﹣1.
练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
